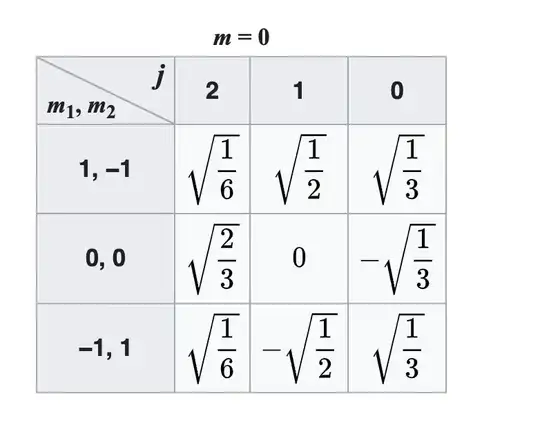
Reference:https://en.wikipedia.org/wiki/Table_of_Clebsch%E2%80%93Gordan_coefficients
The above picture is when $j_1 = 1$ and $j_2 = 1$, why do there exist three values for $j$? I know when $j = 2$,it is $j_1+j_2$, when $j = 0$, it is $j_1 -j_2$, so what is the situation for $j = 1$? Can someone help me out, thanks!
I believe you may be confusing the magnitude of angular momentum $j$ and its projection onto the $z$ axis $m_j$. The table shows you how to combine two angular momentum of magnitude $j_1 = j_2 = 1$ such that the total projection onto the $z$ axis is zero $m = 0$. This can be done in the three ways summarized in the table, e.g., $\lvert j=2, m=0\rangle = (\lvert m_1 = 1, m_2 = -1 \rangle - \lvert m_1 = -1, m_2 = 1 \rangle ) / \sqrt 2$
