How much pressure would it take to compress a block of solid steel into one-tenth the original volume?

Question

We all know to compress objects into smaller volumes, you would need to apply pressure to them. The required pressure depends on how strong the material is and which form is it (gas, liquid, solid).

I have a 10 cm3 block of steel in my room. I am always wondering how much pressure it would take to compress my steel block into one-tenth of its original volume.

If I built a special custom hydraulic press that could press on all sides, would it be strong enough? I have asked websites such as Reddit and Quora, but they never answer that correctly.

Answer 1

The basic answer is "Perfectly achievable pressures, but not for very long (with lasers, it's even legal)"

Metal is perfectly happy to shrink if you squeeze it hard enough. This is in fact the way that fission based plutonium nuclear bombs are detonated: the plutonium pit is squeezed to around 1/3rd its original volume by carefully timed explosive charges. (How much does the radioactive core of a nuclear bomb shrink due to compression by conventional explosives before it goes critical?)

On a related note, if you do successfully build an explosive vice to shrink your steel cube, be aware that you will probably have grey suited visitors.

I did notice that you asked for 1/10th the original volume, not merely 1/3rd. For this, conventional explosives won't really suffice. The solution to this conundrum is of course, more nuclear science. A fusion type nuclear weapon squeezes its secondary core using x-ray radiation from an initial fission explosion. The W-80 nuclear weapon allegedly reaches pressures of 140 TPa, https://en.wikipedia.org/wiki/Thermonuclear_weapon#Radiation_pressure . If you steal a w-80 and swap in your cube for the lithium deuteride fuel and then set it off, it will be adequately squeezed.

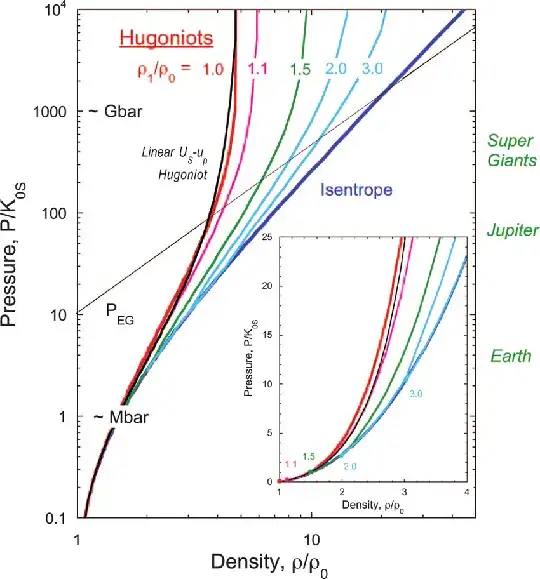
Finally, you could use lasers! Here's the chart of squeezing iron with lasers, they get it up to ~2x its original density at 1 TPa, but pressure required to increase density is rapidly increasing. 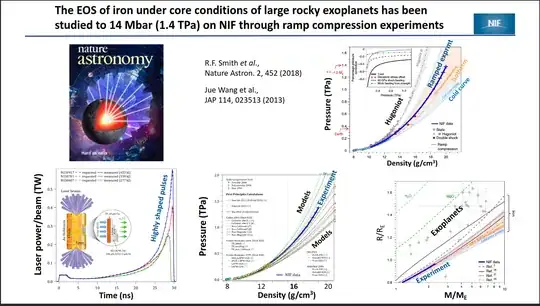https://www.osti.gov/servlets/purl/1860794 However, this isn't nearly the peak pressure achievable at the National Ignition Facility. The top right graph only goes to 1 TPa because that's what's relevant for exoplanet studies. This experiment isn't even an implosion, they just hit one side of the sample with the laser/ Their fusion studies get to 100,000 times higher pressures and compress hydrogen to 100 times the density of lead, so they could very easily compress steel to ten times the density of steel https://en.wikipedia.org/wiki/National_Ignition_Facility. The disadvantage of this approach is that it could only compress a small portion of your cube, while the "steal a nuke" approach could probably squeeze the whole thing.

Answer 2

The basic answer is "no, you cannot." Consider that if you have enough pressure to compress an "incompressible" steel to one tenth its volume, the surfaces doing the pressing experience the same forces, but in only one direction. The surface of your hydraulic piston will literally squeeze out the sides before you compress the steel.

But if you really want a number, we can make a ballpark estimate. Steel typically has an elastic modulus of 200 GPa. The pressure needed to deform this steel to 1/10th its size would be 10 times that much, 2TPa. That's a gross estimate, missing out on an astonishing number of factors. I would expect the real answer to be higher, but this is at least a number we can work with.

Turning to Orders of Magnitude (pressure), we can find pressures to compare against. The highest pressures we achieve in a diamond anvil are on the order of 0.6TPa. 5TPa is the kind of pressure we see in fusion experiments. Since I am certainly discounting all sorts of non-linear effects, it is very likely that you will reach the point of fusing atoms together before you generate the kind of compression you seek.

Answer 3

The bulk modulus of steel is 160 GPa, meaning that if it were linear, it would take 160 GPa to compress it twice. The pressure at the center of Jupiter is up to 7 TPa, which would be sufficient to compress steel 40 times, if the pressure/density relationship was linear.

It's not linear. Compressing matter 10 times takes even more pressure. Still, at some point, inside a large enough celestial body, it will be possible.

No need to ruin a perfectly good hydraulic press. It's literally as easy as flying to the nearest supergiant, dropping off your block of steel, and whistling casually like you have no idea how it got there.