Water pressure at the bottom of a box changes drastically depending on whether a water column above is connected or not?

Question

(For the purposes of this question I'm ignoring atmospheric pressure completely)

Consider a hollow cubic box with side length $1\text{m}$ that we fill up with water. Now suppose we make a small opening of $1\text{mm}^2$ and on top of this we attach a square rigid pipe of length $1000\text{m}$ and cross sectional area also $1\text{mm}^2$ (so its cross section has $1\text{mm}$ long sides). This pipe holds $1000\text{cm}^3 = 1\text{L}$ of water. When we fill up both the box and the pipe with water the pressure due to the water at any point on the bottom of the box will be $\rho gh = 1000\times9.81\times1001 Pa = 9.82 \text{MPa}$

However now if instead of cutting a hole in the box and then placing the pipe on top of it I instead just fill everything with water and place the pipe on top of the box (so that there is no way for water to move from one to the other) then what I have is just a $1\text{m}^3$ box full of water with a $1\text{kg}$ mass on top of it (the mass of the full pipe) which puts a force of $g = 9.81\text{N}$ on the top of the box. Since the water at the top of the box must have sufficient pressure to resist this force and the area of the top of the box is $1\text{m}^2$, the pressure at the top of the box must be $9.81/1 = 9.81Pa$ and therefore the pressure at the bottom of the box will be this pressure plus the pressure from $1m$ of water (which is $\rho gh = 9.81 \text{kPa}$) which totals to only $9.82 \text{kPa}$.

(See diagram below showing these two cases pictorally)

This seems very strange to me: if we don't cut out the $1\text{mm}^2$ hole then the pressure at the bottom of the box is $9.82 \text{kPa}$, but if we do make this tiny cut the pressure suddly jumps up by a factor of $1,000$, turning into $9.82 \text{MPa}$. This is so unintuitive to me that I feel like I must be doing something wrong here. So, where exactly am I messing up, or should I be updating my intuition?

Answer 1

Your calculation is correct; the pressure does increase when you cut the hole. Here's an example that might help illustrate:

Put some water in a cubical box of side length 1 meter. The pressure at the bottom will be 10kPa, as you showed. If you seal up the box tightly, maybe leaving a little air at the top, and bring it to the bottom of the ocean, it will stay at the same pressure—the air inside a submarine doesn't change pressure as you go down. This is the situation when you don't cut the hole.

Now imagine you didn't close the box entirely before submerging it—it doesn't matter if you left the whole top off or left a tiny, millimeter-sized hole at the bottom, so long as the box isn't watertight. If you take that box to the bottom of the ocean, water will rush in if you left any air, and the pressure of the water inside will be the same as the pressure of the water at the bottom of the ocean outside.

Answer 2

Update: In writing this, I assumed the box to be perfectly rigid (except in the penultimate paragraph, where I still take it to be almost rigid.) In doing so, I overlooked the fact that, when calculating the pressure in the box when the tube is filled but sealed, the author tacitly assumes that either the box walls are not, or the box is actually a piston-in-cylinder arrangement (and ignoring the mass of the apparatus). I'm assuming that the intention was for the box to be taken as perfectly rigid: doing so does not eliminate the paradox, and it makes it easier to explain. For an in-depth discussion of how a non-rigid container complicates matters, see Ilmari Karonen's reply.

The situation is essentially the same if we have a valve at the bottom of the pipe where it enters the box, so we can do the following:

1. Fill the box up to the level of the valve. The pressure at the bottom of the box is essentially the same as you have calculated in your second scenario.

2. Close the valve and fill the tube. With the box isolated from the tube, the pressure within it will be unchanged, while the pressure on the tube side of the valve will be 9.81 MPa, as you would expect.

3. Open the valve. Now the pressure in the pipe is being applied to the water in the box. If the water is perfectly incompressible and the box is perfectly rigid, you will get the situation in the first scenario.

In practice, the box will expand slightly and consequently the water level in the pipe will fall somewhat, but then water can be added to bring it up to the original level, restoring the pressure to that which you have calculated for the scenario.

It may be a useful exercise to calculate, for each scenario, the net downwards force exerted by the water on the top and bottom inside surfaces of the box (plus that on the valve when it is closed), to see that, in all cases, it is equal to the weight of the water in the apparatus.

Answer 3

Imagine that every molecule of water is a little person trying to squeeze onto a busy train car.

In the case where there is a hole in the pipe, it's like the train car doors are open and passengers are trying to get onboard. If any person already on the train makes a little more room, then a new person at the door can get onboard. Consequently, every passenger is affected by the existence and urgency of those trying to board. If there are millions of people all pushing to get onboard, those already on the train must exert an enormous force to keep them out. At equilibrium, nobody is moving across the door's threshold, but they have the potential to do so, and that potential causes pressure inside the car.

In the case where there is no hole, and crucially you've stated that the pipe is rigid (it would be different for a flexible membrane), it's like the train car doors are closed. If a passenger onboard briefly makes a little more room, perhaps by sucking in their belly or folding their shoulders together, nothing significant changes; no one else can board the train because the doors are blocking the path from the outside. So the passenger relaxes again; they do not "feel" the presence of anyone outside the train, and the only pressure they experience is due to the people inside the train.

(The linked question has a related explanation that evidently doesn't resolve the conundrum; this answer is an attempt at a slightly different analogy.)

Answer 4

A major issue with your thought experiment is that, in your two scenarios, you seem to be making two different and contradictory assumptions about the rigidity of the box (and/or the compressibility of the fluid).

---

In your first scenario, you seem to be implicitly assuming that the walls of the box (and the pipe) are perfectly rigid. If the top and sides of the box can deform even a little bit under the enormous pressure of the 1 km column of water, they'll flex outwards and expand the volume of the box until most of the water in the pipe (of which there is only one liter) has flowed into the box, drastically reducing the pressure.

In your second scenario, however, your reasoning only works if the box is not perfectly rigid. If it was, the weight of the pipe on top would be supported fully by the box, and none of it would be transferred into the water inside the box. Instead, you seem to be assuming that the top of the box is effectively floating on the water inside, so that the full weight of the pipe is transferred to the water.

---

Furthermore, if the box was perfectly rigid, fully closed and filled with incompressible fluid, the pressure inside in scenario 2 would actually be indeterminate! You can see this by observing that, since the box is rigid and the fluid incompressible, we can fill the box with fluid to any pressure before sealing it, and the volume of fluid inside the box will be the same! Thus, under these assumptions, just knowing the shape of the box and the amount of fluid inside is not enough to determine the pressure.

Obviously that's not a physically meaningful scenario, but we can regard it as an approximation of a situation where the box is almost rigid and/or the fluid almost incompressible.

In particular, let's assume that there's a valve at the top of the box, where the pipe will connect, which we can open and close at will.

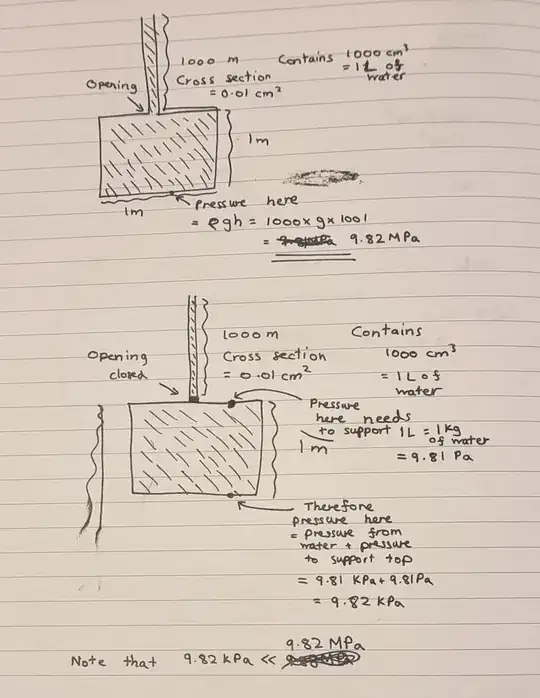
We will first remove the pipe and pour water in through the top valve until the box is full of water and the pressure at the top of the box equals ambient pressure. As you've calculated, the pressure at the bottom of the box will then be (ambient pressure plus) 9.81 kPa, i.e. the pressure under one meter of water.

If we now close the valve, the pressure inside the box will not change. Now we plug in the 1 km × 1 mm² pipe into the (closed) valve and fill that with water too.

The pressure at the bottom of the pipe (above the closed valve) will now be 9.81 MPa. (We assume the pipe and the valve somehow withstand this pressure.) The only thing that has changed below the valve, however, is that there's now an extra 1 kg weight of water (plus the weight of the empty pipe itself, which realistically would of course be way more than 1 kg) resting on top of the box.

Since we assumed the box to be almost perfectly rigid, we can assume that the box will support most of this weight by itself, and thus the pressure of the water inside should not appreciably change. However, even if the entire weight of the water column was somehow transferred through the top of the box to the water below — maybe the "top" is actually a piston supported by the water below, but otherwise free to slide up and down? — that would still only increase the pressure inside the box by 9.81 Pa, i.e. from 9.81 to 9.81981 ≈ 9.82 kPa.

Now let's open the valve. What happens?

If the top of the box was actually a floating piston (of negligible mass, just like the pipe), what would happen is that the liter of water in the pipe would simply drain into the box, while the piston would rise by 1 mm to accommodate it. The pressure at the bottom of the box would still be 9.82 kPa just like before opening the valve.

However, let's go back to our initial assumption of a nearly rigid box. When the valve is opened, the 9.81 MPa pressure at the bottom of the pipe is now transferred to the water in the box, and through it to the sides of the box. That's a lot of pressure pushing the sides outwards, and since they're only almost rigid, they'll still deform a little. And they only need to move a fraction of a millimeter for the box to expand enough to fit the extra liter of water from the pipe.

Even if the walls of the box were really rigid, and could withstand a pressure of nearly 10 MPa without moving even a fraction of a millimeter, the water in the box is only nearly incompressible. The bulk modulus of water is around 2.2 GPa, so at a pressure of 10 MPa the volume of water decreases by about 0.45%. Since the volume of the pipe is only 0.1% of the volume of the box, however, that's more than enough for all the water in the pipe to fit into the box even without the walls flexing at all.

Of course, as water drains out of the pipe and into the box, the pressure in the box will drop until the system attains an equilibrium, with a pressure at the bottom of the box somewhere strictly between 9.82 kPa and 9.82 MPa.

The exact equilibrium pressure depends on the rigidity of the box and the compressibility of the fluid in it. Assuming a perfectly rigid box and a bulk modulus of 2.2 GPa for water, we can in fact calculate the equilibrium height of the water column as about 180 m, with a pressure at the bottom of about 1.8 MPa, which is enough to compress the volume of the water in the box by about 0.08%, or just enough to accommodate the extra 820 ml of water drained from the pipe.

---

Ps. What if we now close the valve again?

The pressure on both sides of the valve is now the same, so nothing really changes. The box still contains approximately a cubic meter of water under high pressure (up to 1.8 MPa, which is a lot, but nowhere near the 9.8 MPa we'd get for the open-valve equilibrium pressure if we assumed the water to be perfectly incompressible and the box perfectly rigid), while the pipe still has enough water in it to maintain the same pressure on the other side of the valve (i.e. a column about 180 m high, which is also a lot, but nowhere near 1 km).

Answer 5

Your calculations are right, so you have do change your intuition. But the principle is used in many hydraulic presses or hydraulic jack.

Answer 6

No, you're exactly correct, and this is one of the variations of the so-called Hydrostatic paradox ("paradox" in the original sense of the word: something that looks counter-intuitive or wrong, but is actually correct). Allegedly, Pascal himself used some variation of this setup to demonstrate the Pascal's law.

Answer 7

Other answers have confirmed that the calculation is correct based the assumptions of the problem, so I thought I'd add something more about why it's an un-intuitive answer. As Joker_vD mentioned in their answer, its an example of the Hydrostatic paradox (which I didn't know the name of).

In reality where all boxes have some flexibility, then adding just enough water to fill tube would gradually increase the pressure in the box as you pour it, and due to that increased pressure the box material would flex and stretch, increasing its volume to accommodate almost all of the water from the tube. By the time you finish pouring that litre of water the height and pressure would only have increased very slightly.

You would need to pour much more water into the tube to actually fill it all the way to the top, assuming the box didn't just explode first as the pressure rises.

When you finished the force on the top of water would come not just from the water in the tube but from the tension within the material of the box - the top surface of the box would be pushing down on the water with a force of about 9,810,000 newtons, equivalent to a weight of 1,000 metric tons. This force corresponds to the tension in the vertical sides of the box.