Will just the increase in height of water column increase pressure or does mass play any role in it?

Question

As we know pressure exerted by any liquid at any given point in a container can be calculated by the formula $P = \rho g h$. Product of density of fluid, acceleration due to gravity and the depth from water surface.

For instance let's assume a tank of capacity $1\mathrm{m}^3$ which has a height of 1 m. The water pressure at the bottom of the tank will be $9.81$ kPa. Now a pipe of height $99$ m and a capacity of just $1$ litre is connected to the top of the tank and filled with water. Now the head of water acting on the bottom of the tank is $100$ m thus the pressure should be $981$ kPa.

Can someone explain how just 1 litre of water exert so much pressure? Also if the tank maximum carriage pressure is $100$ kPa, will the tank rupture?

Answer 1

At first, the conclusion seems absurd. You have a tank, which is open at the top of the pipe, that is comfortably holding 1000 L of water. Then you add just 1 L more, albeit in an unusual shape, and it bursts! How can this be?

(At first, we will assume that the tank is perfectly rigid and that water is perfectly incompressible. Later we will relax those assumptions.)

To see why, let's first take this to an extreme, and imagine that the pipe is just one water molecule wide, but still contains 1 L of water. (The pipe would be so long that Earth's gravitational field can't be treated as constant along its length, but ignore that. As pointed out by Philip Roe's answer and Dast's answer, the water molecules would stick to such a narrow pipe; ignore that too, and assume they can still slide freely in the pipe.) The weight at the interface of pipe and tank remains a mere 1 kgf or 10 N. No problem right?

But think about what's going on at that interface, depicted in this crude illustration (pretend that water molecules are spherical):

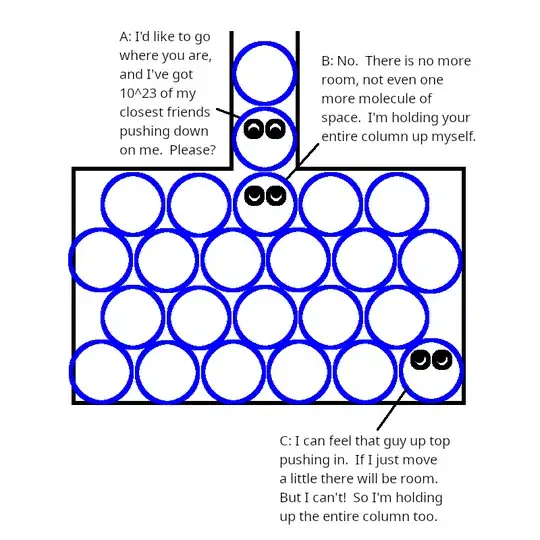
The molecule at the bottom of the pipe (call it A) is trying very hard to get into the tank. It's got an enormous number of molecules above it, pushing to get in as well. That 10 N, ordinarily so easy to hold, is concentrated into a very small area, creating enormous pressure on the molecule just below it. As suggested in Dast's answer, we can think of this column of water as being like an extremely thin needle being pushed into the tank with a force of 10 N.

The molecule below A (call it B) has to hold up the entire column itself. If it could just squeeze a little this way or that way, A could get in. But it can't! B pushes just as hard on all of its neighbors, trying to make just a tiny bit more room, but its neighbors all push back just as hard. There is no room!

You might think that B's neighbors might be able to share the load. But remember that these molecules can easily slide past one another. If even one of B's neighbors (call it D) is not resisting with the full 10 N, then B, propelled by A and sliding past the other neighbors (even at a right angle if need be), will be able to push into D and move it out of the way, thereby making additional room in the tank for A. The chain of forces from A to B to D is sort of like a plumber's pipe snake: the end is pushed forward with essentially the same force as at the start (and for low-viscosity water, rather than pipe snakes, it is the same force).

Even a distant molecule (call it C) can feel the pressure. If C just moved a tiny bit, maybe pushed its way into a crevice or crack, or convinced the tank wall to flex just a little, then there would be room for A. But it cannot! There is no room! Everywhere in the tank, every molecule must resist the full 10 N, otherwise it will be pushed aside since nothing impedes the transmission of forces from A.

The upshot is that column of water really has created enormous pressure everywhere in the tank despite only weighing 10 N.

More realistic assumptions

Let's imagine actually building this tank and pipe configuration and filling the pipe gradually. We'll go back to using 99 m of pipe with a 0.1 square centimeter cross-section area, and allow the tank walls to flex a bit. The tank initially holds 1000 L of water and the pipe is empty. You start pouring water into the pipe. At first, it fills in the way you expect, with the water level in the pipe rising.

But after a short time, the pipe water level stops rising! You keep pouring, but the water level in the pipe doesn't move much. Why? The pressure has built to the point that the water in the tank is starting to deform the tank. It's rated for 100 kPa, but some deformation happens on the way to its maximum pressure. The water molecules also move slightly closer together as the pressure increases; see incompressibility of water.

As you keep filling, the water keeps forcing its way into the tank, flexing the walls ever more to accommodate it. Due to the resulting expansion, you have to pour much more than 1 L to make the pipe water level rise, even though the pipe itself is holding much less than that. The water molecules are trying to push into the tank's crystal lattice, and the tank itself suffers dislocations as it struggles to keep its shape. Meanwhile the water level in the pipe is approaching 10 m, meaning 100 kPa of pressure. Finally, the failure pressure is exceeded and the tank fails. (If it's rated for 100 kPa then we'd hope it fails at more like 300 kPa, but that's an engineering detail.) We can't actually fill the pipe to a height of 100 m unless the tank and pipe are very strong.

Finally, let me acknowledge a few more simplifications I've made:

• In a fluid, the molecules are all in motion, rather than being locked in place. That is part of why pressure is equal in all directions, as the flow allows local pressure differences to equalize. The roles of molecules A and B will be played by different physical molecules at different points in time (and are, anyway, abstractions of layers of molecules in a realistically sized pipe).

• Molecules don't really "touch" each other in the same way that macroscopic objects appear to. For more a sophisticated treatment of the microscopic interactions, I'd refer to the question What does it mean for two objects to "touch"?

Answer 2

The 1 liter pipe only encompasses a tiny fraction of the lid area of the tank. But is has caused a pressure of 972 kPa at the lid, and the lid is pushing downward on the liquid inside the tank with this same pressure. So the bottom pressure of 981 kPa is just enough to equilibrate the vertical forces on the water in the tank.

So, if the failure pressure is 100 kPa, a pressure of 981 kPa will be sufficient to cause failure.

Answer 3

Can someone explain how just 1 litre of water exert so much pressure.

Put succinctly, pressure (compressive equitriaxial stress, with the free surface serving as a reference) is exactly the gravitational potential energy per volume.

For a thinner pipe, you get greater fluid descent in a gravity well when you remove a given volume from the bottom. As a result, the potential change is larger, and so therefore is the bottom pressure.

Also if the tank maximum carriage pressure is 100 kPa, will the Tank rupture?

Sure—pressure is pressure.

Answer 4

Also if the tank maximum carriage pressure is 100 kPa, will the tank rupture?

Yes, the tank will rupture, since the pressure is 981 kPa.

---

Here's one analogy that could help. If you drop a golf ball on someone's head from 1 meter up, it probably won't injure them too much. If you drop a golf ball on someone's head from 100 meters up, it will probably "rupture" their "tank."

The analogy is not so far off since the fixed cross-sectional area of the golf ball is similar to the fixed cross sectional area of the tall pipe. Similarly, both the golf ball and the water have a form of "energy" ($P/\rho\propto PV$ is the rough analogy here for the water) due to changing their position in a uniform gravitational field.

A non-analogy answer is provided below.

Can someone explain how just 1 litre of water exert so much pressure.

Pressure is a force divided by an area.

By creating a really tall column of water in a thin pipe you necessarily have a very small cross sectional area of the pipe. You are dividing by this very small area to obtain the pressure.

Will just the increase in height of water column increase pressure or does mass play any role in it?

Yes, mass plays a role (assuming your pipe and tank full of water are in a gravitational field). All body forces must be accounted for, including the force due to gravity.

Consider, for example, the usual expression for pressure as a function of depth from the top of the pipe ($h$): $$ P=P_0+\rho g h\tag{1}\;, $$ where $P_0$ is the atmospheric pressure at the top of the pipe.

The above Eq. (1) is well known, but do not forget that it is only valid for a system in equilibrium in a uniform gravitational field.

Because the water in your pipe has mass and because it is in a uniform gravitational field, it exerts a force on the water below it.

The water at the bottom of the long skinny pipe feels the full force due to the one liter's mass, which is $$ F=mg=\rho g h A\;, $$ where $h$ is the height of the long skinny pipe and $A$ is its (small) cross-sectional area.

Clearly, the pressure at the bottom of the pipe (and the top of the tank) is $$ P = P_0 + \frac{F}{A} = P_0 + \frac{\rho g h A}{A} = P_0 + \rho g h\;. $$

Answer 5

The cross-sectional area of the pipe doesn't matter. Imagine putting a bunch of these pipes, enough to completely cover the tank. So now we essentially have one super-pipe with area $1 m^2$. Pressure is force per area, and we're multiplying both that mass of the water above, and the area, by the same factor, so the pressure stays the same. So if $1 m^2$ of water produces a certain pressure, then so will a smaller pipe.

It might be clearer if we put it in different units. Pressure is force/area. If we multiply top and bottom by distance, we get (force$\cdot$distance)/volume. (Force$\cdot$distance) is work. So pressure is the derivative of work with respect to volume. That is, to increase volume by $\Delta V$, we need $p \Delta V$ work. That is, if we want to inflate a balloon at the bottom of the tank to have a volume of $V$, we need $pV$ energy (that is, for small $V$; as we increase $V$, we increase the height of the water column and thus increase the pressure, so the exact energy is $\int p(V)dV$).

To inflate a balloon the volume $V$ at the bottom of the tank, we have to displace water, which has no place to go but up, which displaces more water, and so on. The only place for the water to go, ultimately, is to the top of the tank. So the only way to inflate the balloon is, on net, to move a volume $V$ of water $100 m$ up (by "on net", I mean that no individual molecule of water needs to go up $100 m$, but the total effect has to be the same as some $V$ of water going up $100 m$). The increase in potential energy is then $(\rho V g)(100m)$, thus the pressure is $(\rho g)(100m)$.

The width of the pipe is irrelevant; expanding the balloon is always going to require moving the same amount of water the same height, regardless of the width of the pipe used to move the water. The crucial part is that the nearest empty space that the water can go is $100m$ up.

Answer 6

Pressure is not simply force (otherwise we'd just call it "force"), but instead is the result of force being applied to an area. If we change the area, we can change the pressure for the given force. Think about pressing on drywall with your thumb, versus pressing on it with the tip of a thumbtack. Which one much more easily makes a hole?

Thus, if changing geometry can affect pressure in that case, even without any further analysis of the problem under consideration, one can then generalize that to not have so much of an intuitive problem with there being a difference in the effects of the same amount of force under two different circumstances when liquids are involved, too. Your tank, in effect, is doing to the weight of the water just what a thumbtack does to the force from your thumb.

(For a more mathematical analysis, one can consider this as related to the idea that the surface area and volume of a container can actually be varied independently by suitably choosing the shape. In particular, it is possible to make the surface area asymptotically approach zero while the volume stays constant, and making the container taller and skinnier is exactly how [or one way of how] you do that.)

Answer 7

I like Scott McPeak's answer. But I thought I would add one extra way of thinking about it.

Imagine we have the 1m cubed of water, and that the tank is completely full, with no wiggle room at all. Further assume their is no way for the water to increase further in density.

Then, we come in with a tiny sewing needle. We try to push it into the tank (through a watertight hole), but obviously it won't go, because the water can't be compressed further. So we push harder, we can get some kind of giant construction machinery and push this needle super-duper crazy hard.

If we keep pushing, the tank will rupture. The water can't get smaller, so eventually all that umph we are putting on the needle breaks the tank.

The fact that its a needle, not a piston, doesn't change the basic result. Your very narrow tower of water is a needle, just one made from water instead of metal.

Caveat - Edge effects

One tiny caveat. With any realistic, real-life, tube the water molecules on the edges of the tube will experience a lot of contact forces with the tube itself. So all the water within a certain distance of the edge should be neglected. For a large system this edge effect is negligible, but if you went all the way to a 1-atom wide tube then it is 100% edge, and the actual downward pressure would be much, much less than you would expect if you didn't account for this. I think the effect would kick in long before then, I have seen the meniscus on a water beaker with my own eyes so it can't be much smaller than 1mm, so that kind of length scale is probably the ball park where these edge effects dominate.

Answer 8

This really is a nice question on which to test ones understanding of fluid presure but it has generated more confused thinking per square inch than I would have supposed possible. It was a good idea to consider a narrow tube, but a mistake to make it so narrow that the fluid can no longer behave like a fluid. Molecules in a fluid exert a force on their neighbors by jostling against them. Imagine that you are giving a child a ride on your shoulders and bouncing them up and down. The tube can be very narrow and still allow room for this. Lets use a tube with a diameter of 1mm and a length 100 m, so a volume of $3.14 \times 10^{-4} m^3$. There will be a lot of friction in this tube so pressure will take time to work along it, but eventually the pressure at the bottom of the tube will reach 981kPa. This pressure will be transmitted throughout the tank by molecular jostling. But water is slightly compressible. Based on a bulk modulus of $2.2\times 10^9$ it would want to change volume by 4.5%, and if it did that by forcing the tank to expand, it could easily accomodate all of the water in the tube. (In fact the level of water in the tank would fall a little!) The shear strain due to this is 1.5%, which I think is well below the rupture strain of mild steel but above that of aluminum alloys. So an aluminum tank would rupture but a steel tank would not.

You can easily repeat this calculation with different diameters of tube. As you increase the diameter, the amount of water needing to enter the tank will increase, and so will the resulting strain, eventually exceeding the rupture strain of any feasible material.

ADDITION

AS Scott Peak and timeskull have pointed out, the hydrostatic pressure will only reach its its theoretical value if the pipe is kept topped up, if it is, the pipe itself might rupture. The pressure to cause this is easily calculated. Suppose the pipe is split in half and then glued back together. The force per unit length driving the halves apart is $2Pr$, where $P$ is the excess pressure, and $r$ is the internal radius. If the stress in the glue joint is $\sigma$ we have a force $2\sigma t$ holding it together, So the glue joint, or the original pipe itself, must be capable of withstanding a stress of $Pr/t.$ We can do a similar calculation for a spherical tank, when the two forces are $\pi r^2P$ and $2\pi rt\sigma$ leading to a critical stress of $Pr/(2t)$. For a cubical tank the stresses will not be uniform and the calculation will be more difficult, but this probably improves over my original analysis of the strain.

Answer 9

I think it's actually more insightful to consider this scenario turned upside-down: you start with a $100\:\mathrm{m}$ thin tube containing only $1\:\mathrm{kg}$ of water. Not much mass, but we know it creates a pressure of $981\:\mathrm{kPa}$.

Let's say the pipe is like a (very narrow) well, vertically underground. It's already full, but then you add more water on top. Much more, $999\:\mathrm{kg}$. Does this thousandfold increase of the water mass increase the pressure at the bottom thousandfold?

Of course not! Because the additional water doesn't stay over the original $10\:\mathrm{mm}^2$ footprint of the pipe's bottom, instead it spills over the rim of the tube and spreads out over the ground as a shallow puddle. Even if the pipe is in this puddle, most of the weight of the puddle is not supported by the top layer of water within the pipe, but directly by the ground. Only the little bit of water that's actually above the pipe contributes to increasing the pressure.

Now think of it again inverted: you have this big but shallow tank. There's a lot of mass of water in it, but this mass is distributed over a large area like with the puddle we had on top, so the pressure is small.

But if you now add the pipe on top, this must again have the same pressure at its bottom as the well did. And if this is on top of the narrow tank, the water inside of that tank needs to have at least as much pressure, else you'd get a flow of water from the pipe into the tank.

Answer 10

You have increased the height of the column of water 100 times, so the pressure ofcourse increase 100 times. Its just that the 100 times factor is for a very small area and the 1 time factor is for a large area (the entire 1 meter square area).

You have two containers, one on top of other. The top container has to be very high and very thin, and you are making it stand on the first container, not lay down on the first container. Consider putting a vase over a table. The table is over a larger, very much larger area of ground than the vase. The vase is placed standing on the table, not layed down on the table.

For the majority of the surface of ground the pressure is just due to the first container. The second container is not top of it so exert no pressure on it.

Consider a water fall. If you are under it your head and shoulders have to experience very high pressure. Move one step sideways and you are away from the water fall, now your head and shoulders are free from the pressure.

The second container has to be very thin because its 99 m long and have just one liter of water. Its volume therefore has to be very small - density of water is fixed and cannot be changed (unless you make it steam or ice but you said water). The volume therefore is also fixed. To have that volume when length is 99 m the surface area that is above the ground has to be very small as compared to the first box.