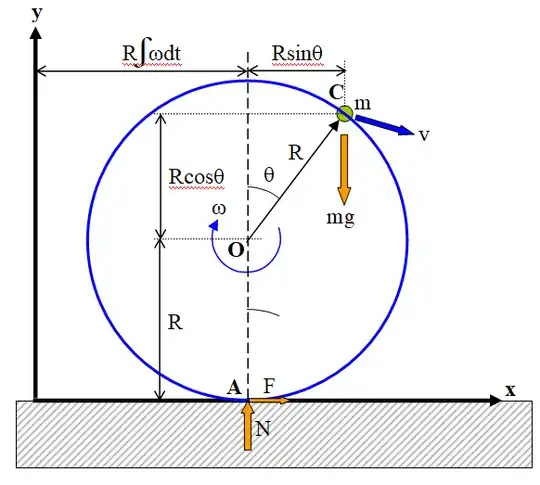
This paper is based on a question by Puk asked Jun 28, 2020 on the Stack Exchange Physics site, Newton's 2nd law for rolling motion with changing moment of inertia, about a long, hollow, rigid but infinitely thin cylinder with a point-like mass in the form of a rod with mass m attached to its wall as shown in the drawing.
Puk states that conservation of energy requires that the angular velocity is
$\omega^2=\frac gR\frac{1-\cos\theta}{1+\cos\theta}$
He does not show any details as to how he gets that result, which implies that the angular velocity becomes infinite at the contact point A where theta is 180 degrees.
I commented that this should be impossible but have received no reaction, so I am asking it here in the hope of a response.
For the sake of completeness I will here outline how I think the conservation of energy method gives that weird result:
The motion in the x-direction is partly translational due to the rolling to the right and partly a displacement due to the rotation around the center O, so
$x=x_0+R\int_{t_0}^t\omega dt+R(\sin\theta-\sin\theta_o)$
In the y-direction there is only a displacement due to the rotation around the center O, so
$y=R(1+\cos\theta)$
The velocities in the x- and y-directions are obtained as the time derivatives $\dot{x} $ and $\dot{y} : $
$\dot{x}=\nu_x=R\omega(1+\cos\theta)$
$\dot{y}=\nu_y=-R\omega\sin\theta$
Their vectorial sum squared becomes
$ \nu^2=2R^2\omega^2(1+\cos\theta) $
Taking the positive square root then gives
$\nu=2R\omega\cos\left(\theta/2\right)$
Using the expression for $\nu$ the total kinetic energy of the system is
$ E_{kin}=\frac12m\nu^2=mR^2\omega^2(1+\cos\theta) $
Overcoming the force of gravity to move the mass m from the contact point A at $y=0$ to the higher position at C with ordinate $y$ requires the work
$E_{pot}=mgy=mgR(1+\cos\theta)$
The total energy $E$ of the system is thus
$ E=E_{kin}+E_{pot}=mR^2(\omega^2+\frac gR)(1+\cos\theta) $
Conservation of energy implies that $E$ has some constant value. Here we let $E=2mgR$ which is the potential energy at the top where $\theta=0$ and where we have chosen to let $\omega=0\:.$
Using this value of $E$ we get
$ \omega^2=\frac gR\frac{1-\cos\theta}{1+\cos\theta} $
which becomes infinite when theta is 180 degrees ??!
With this expression for omega we get
$ E_{kin}=mgR(1-\cos\theta) $
which of course is finite for any value of theta.