My intuition says 'no'. I know from my knowledge of spaceflight that every orbit includes the point at which delta-v was last spent; you can't use only a cannon on the ground to put something into a stable orbit because the last point delta-v was applied is on the ground.
I would think a similar limitation would apply to the photon sphere as well. Or am I way off and photons really can get stuck in the photon sphere?
Yes and no. ;)
In this answer, I'll only discuss photon trajectories in the Schwarzschild metric. Trajectories around Kerr black holes are more complicated. I'll use units such that the Schwarzschild radius equals $1$.
Schwarzschild photon trajectories can do things that aren't possible in Newtonian gravity. In particular, a fast body in Newtonian gravity gets deflected in a hyperbolic trajectory. However, in GR, a photon can make one or more loops around a black hole (or neutron star) before travelling on.
We can describe the trajectory in terms of the impact parameter $b$: the closest distance from the trajectory to the centre of the BH if there were no gravity.
The critical impact parameter is $b_0 = 3\sqrt3/2 \approx 2.59807621$. If $b>b_0$ then the photon is deflected. If $b<b_0$ the photon will fall below the photon sphere and cross the event horizon. In either case, the photon can make a number of loops around the BH. The closer its $b$ is to $b_0$, the more loops it makes. So if $b$ is very close to $b_0$ it can make an arbitrarily large number of loops.
Here's a trajectory with $b=3.62001264240871876$, which gets deflected by $60°$.
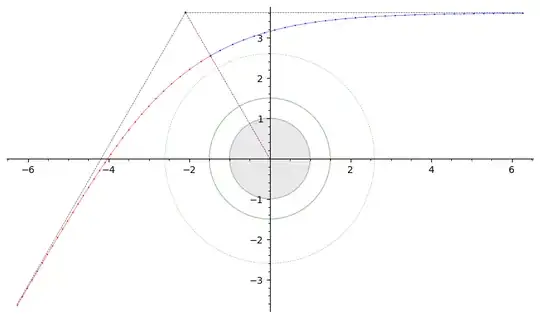
The greenish circle at $1.5$ is the photon sphere. The radius of the dashed circle is $b_0$.
Here's a trajectory with $b \approx 2.59807621533240768089$, which gets deflected by $1140°$. So it's similar to the previous trajectory, except that it does 3 loops before escaping.
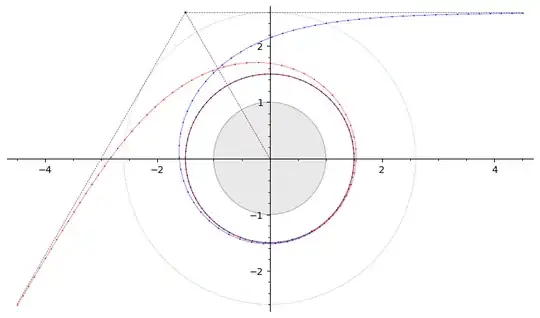
Both of these trajectories were calculated using Carlson's algorithm for evaluating elliptic integrals, with high precision arithmetic. (The dots on the trajectories are computed using elliptic integrals, the connecting curves are cubic Bézier curves).
I have further details and diagrams in this answer, and this more recent answer.
So on first analysis, a photon trajectory with impact parameter $b=b_0$ feeds into the photon sphere and stays there indefinitely. However, that orbit is unstable. The slightest perturbation will throw the photon out of the photon sphere. So indefinite photon sphere orbits are purely theoretical. They can only happen in a universe with no perturbing influences.
But on further analysis, the photon cannot orbit indefinitely even in those ideal conditions. The photon-black hole system radiates gravitational radiation, so the orbiting photon is doomed to fall out of the photon sphere. Of course, the power of that radiation is ridiculously tiny, even compared to the energy of a single photon. But it is non-zero, so we can't neglect it.
As I mention in the 1st linked answer above, in Divergent reflections around the photon sphere of a black hole, (published in Scientific Reports, a Nature Portfolio journal), Albert Sneppen gives a nice equation for the number of loops (originally given as Eq. 269 in Chandrasekhar's The Mathematical Theory of Black Holes). Let $b=b_0+\delta$. If this trajectory makes $n$ loops then the trajectory with $b=b_0+\delta e^{-2\pi}$ is almost identical except it makes $n+1$ loops. This applies to both trajectories with $\delta>0$, which escape, and to trajectories with $\delta<0$, which end up plunging into the event horizon. The trajectory with $b=2.6013402014052278804$ is deflected by almost exactly $360°$, i.e., it makes one loop before continuing on its original path.
An intuitive reason why a spacecraft cannot enter into a circular orbit without accelerating itself is that a time-reversed trajectory is also a valid trajectory. Thus, if an unaccelerated spacecraft could enter a circular orbit, then an unaccelerated spacecraft already on a circular orbit could spontaneously depart from that orbit. We know this cannot happen: Newtonian circular orbits are stable.
However, photon orbits in the photon sphere are unstable, meaning that small deviations are exponentially amplified over time. So a photon on an (arbitrarily close to) circular orbit does indeed depart from that orbit, either escaping the system or falling into the black hole. And so, by time-reversing that picture, a photon arriving from far away can indeed enter into an (arbitrarily close to) circular orbit.
Of course, the instability of these orbits also means that a photon is highly unlikely to remain "stuck" in the photon sphere for long.
The photon sphere is a mathematical construct. Infinitely thin.
Now, photons are quantum objects, so photons have an uncertainty in location and momentum. So either a photon is not on the photon sphere, or it is not moving along the photon sphere. In either case, it's not going to stay there.
You can't use your Newtonian intuition. The effective potential of light in the Schwarzschild metric has a local maximum, which does not exist in Newtonian gravity. If light arrives at $1.5r_s$ with exactly the right ratio of energy to angular momentum such that it has no inward motion, then in principle it can enter a circular orbit.
The magic number is an impact parameter of $3\sqrt{3}r_s/2$ and the closer to this value, the more "orbits" the light will make before either falling inwards or heading outwards to infinity.
