The inner workings of the Olbers paradox

Question

A long time ago I was told that the universe is finite. The provided "proof" (or reasoning), known as Olbers' paradox, was that on infinite universe there would be an infinite number of stars, and that an infinite number of stars in night sky would make the sky bright.

I guess this sounds reasonable, but I have some doubts. If we assume that universe really is infinite and that it has infinite number of stars spread somewhat uniformly on the space, how would one prove (or disprove!) that the night sky really would be bright? What assumptions one would need to make on the way constructing the proof?

I am not looking for a "correct" answer but how to approach the claim mathematically.

Answer 1

I have nothing to say about the (possible) infinity of the universe; however, it is the case that infinitely many stars distributed uniformly will create infinite brightness at any point.

Let's throw away all the real physical facts about stars, and make the (incorrect, but good enough for now) assumption that the universe is an infinite volume with some 'star' distributed uniformly throughout it. So there is a uniform 'brightness field' which I'll denote by $\phi$.

Now suppose we are standing at the point $\mathbf 0$. How much brightness are we getting from a small volume $dV$ at a distance $r$ from us? Well, the small volume is emitting light rays at an intensity of $\phi dV$, but as you get further away (say, at a distance $s$) from the volume, the light rays are spread over the surface of a sphere of radius $s$. The surface area of a sphere of radius $s$ is proportional to $s^2$, so the light intensity due to the volume at a point a distance $r$ away from the volume is proportional to $\frac{1}{r^2}$.

_{(source: ohio-state.edu)}

So the volume $dV$ contributes a brightness of $\frac{C}{r^2}dV$ to the total brightness, where $C$ is some constant, and $r$ is the distance of the small volume from $\mathbf 0$. We are now in a position to integrate over a large sphere of radius $R$ to get the brightness due to all the 'stars' at a distance less than $R$ from us:

\begin{align} \textrm{Total brightness at distance less than $R$} &= C\int_{|\mathbf x|<R}\frac1{|\mathbf x|^2}dV\\ &=C\int_0^{2\pi}d\phi\int_0^\pi \sin(\theta)d\theta\int_0^R\frac1{r^2}\times r^2dr\\ &=C\times4\pi\int_0^R dr=4\pi CR \end{align}

So the brightness due to the stars in a sphere of radius $R$ is proportional to $R$. Clearly, if we make $R$ infinitely large, the brightness will become infinitely large as well.

Of course, this ignores several physical realities, such as the expansion of the universe, the geometry of space-time, etc. But that is, at least, the mathematical justification for your friend's claim.

Answer 2

There is one thing that you have failed to consider: the expansion of the universe. Since the expansion of the universe is "faster" the further away it is from us, there will come a point where the expansion is faster than the speed of light. (This actually happens, I'll add sources if I have the time to do so.) So, the light from stars at or greater than that distance would not be able to reach us.

Secondly, since infinite time has not elapsed, not all light have reached us.

Edit: great video to answer your question
http://www.youtube.com/watch?v=gxJ4M7tyLRE

Answer 3

Answers ignoring the effect of interstellar matter, modeled here by the Beer-Lambert attenuation law, are incorrect. The assertion that Olbers's Paradox proves a finite size of the universe is severely anachronistic and embarassingly outdated. Olbers himself disregarded this law as it was not documented with respect to stellar light until 1930, more than a century after he proposed this supposed paradox as a thought experiment. Why didn't they notice it before? Well, they couldn't see it, so many assumed it was not there. It is simply that there is indeed non-luminous material between stars, in seemingly "empty" space, and that light intensity is known to decrease according to an exponential decay curve as it travels through such matter. Those arguing otherwise are asking us to presuppose the non-existence of planets, moons, asteroids, dust and gas (from which the stars themselves are said to form), nebulae, dark matter, etc.

I have written a basic simulation to validate the effects of non-luminous matter quantitatively and qualitatively. Code here. It directly applies the exponential decay law by assuming a uniform random density of stars and a uniform density of non-luminous matter throughout space. The simulation even cheats massively in favor of Olbers's Paradox by modeling the infinite backdrop of stars at varying distances as a purely luminous wall of light at a fixed, finite and even shortest possible distance beyond the foreground model of direct sampling. This means we have a strict theoretical upper bound on the total light emanating from distant stars. The density of non-luminous matter is controllable as a parameter p. The simulation shows that for even very small values of p, a purely luminous wall would be practically invisible, or else be completely indistinguishable from cosmic microwave background radiation (interstellar attenuation not only decreases apparent intensity, it also induces reddening).

In other words, Olbers's thought experiment would fail to falsify even the hypothetical existence of a contiguous sphere of light as luminous as the surface of the brightest star enveloping the entire visible portion of the universe. It can say nothing about what is beyond the photons that reach us.

If one sets p=0, the entire field of view is indeed saturated by pure, contiguous starlight under this simulation. But for any non-infinitesimal density p of attenuating matter, the visualization -- and the mathematical solution for expected light intensity over all points in space--converges sharply towards a model that perfectly resembles what we see in our night sky, regardless of all other parameter settings.

In the following two images, the absorption value is increased only slightly, starting as close as the simulation allows to zero at first:

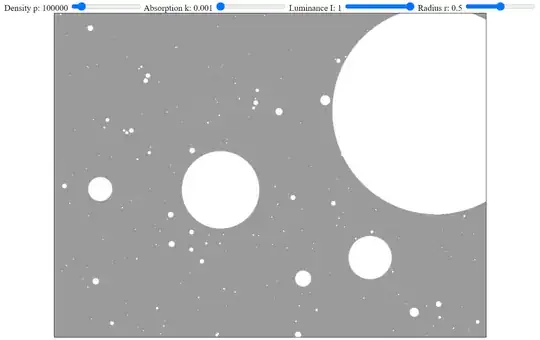
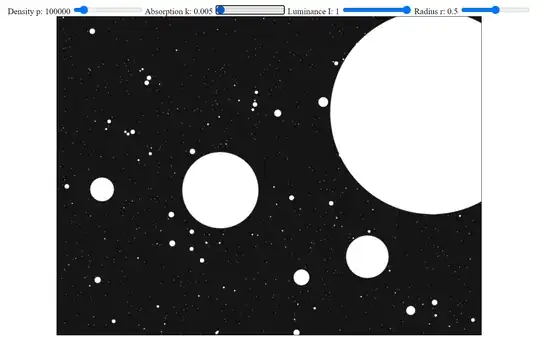
In both images, there is a perfectly bright wall of simulated stars a short, fixed distance away from the observer. Radiation from that wall leaks and is visible as a uniform grey background when the simulated wall is very close and the density of attenuating matter approaches zero, but if the wall of light is slightly more distant or the density of attenuating matter is only slightly increased, the background approaches pitch black, despite there still being an infinite number of perfectly bright stars intersecting every possible line of sight.

In case you think this idea is flamingly absurd, that even a small amount of matter between stars can block nearly all of the light from them, remember that despite how brightly the Sun shines at noonday and how close it is to the Earth, you can block almost all of that light using a thin cardboard cereal box or a parasol consisting of cloth a couple millimeters thick. This gives you an idea of how effective exponential attenuation is. Can there not be the equivalent matter of one millimeter of cardboard between you and a star 3 billion light years away? If not then what are stars made of?

Answer 4

If all photons decay after some arbitrarily large time period, Olbers paradox is no longer an objection to the proposed infinite extent of the universe.

Answer 5

There are things that block out brightness (relative brightness). The sun is the brightest star during the day, and most stars are way too faint and distant to notice them as bright.