There is no paradox, even under classical physics.
Olbers posed the supposed paradox in 1823.
It wasn't until more than a century later that interstellar extinction, or the attenuation of light due to non-luminous matter absorbing photons, was formally documented.
Olbers's Paradox consequently actually fails to demonstrate a finite or nonuniform universe, by failing to account for a now-known phenomenon of light extinction.
Matter is known to attenuate light according to an exponential decay law (see the Beer-Lambert attenuation law).
The law of optical attenuation had in fact been known, studied and published on by 1729 and before. What had not been as well studied is the role of interstellar matter specifically in obscuring stars. Hence the seeming "paradox" was merely a failure to account for something that is in fact there.
Oddly, those arguing against the existence and prevalence of such matter are asking us to presuppose the non-existence of planets, moons, asteroids, dust and gas (from which the stars themselves are said to form), nebulae, dark matter (upon which modern astrophysical theories rely and even say it is five times as prevalent as ordinary matter), etc.

I have written a basic simulation to validate the effects of non-luminous matter quantitatively and qualitatively. Code here. It directly applies the exponential decay law by assuming a uniform random density of stars and a uniform density of non-luminous matter throughout space.
The simulation even cheats massively in favor of Olbers's Paradox by modeling the infinite backdrop of stars at varying distances as a purely luminous wall of light at a fixed, finite and even shortest possible distance beyond the foreground model of direct sampling. This means we have a strict theoretical upper bound on the total light emanating from distant stars. The density of non-luminous matter is controllable as a parameter p. The simulation shows that for even very small values of p, a purely luminous wall would be practically invisible, or be indistinguishable from low-energy uniform background radiation.
If one sets p=0, the entire field of view is indeed saturated by pure, contiguous starlight under this simulation. But for any non-infinitesimal density p of attenuating matter, the visualization -- and the mathematical solution for expected light intensity over all points in space--converges sharply towards a model that closely resembles what we see in our night sky, regardless of all other parameter settings.
In the following two images, the absorption value is increased only slightly, very close to zero at first:
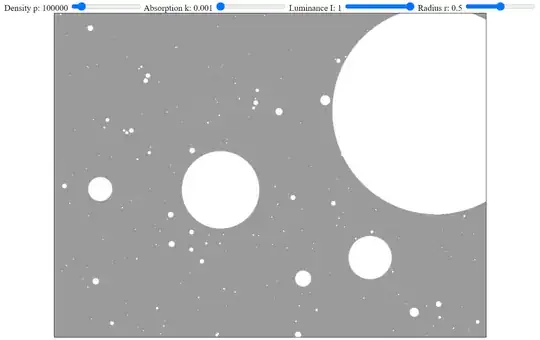
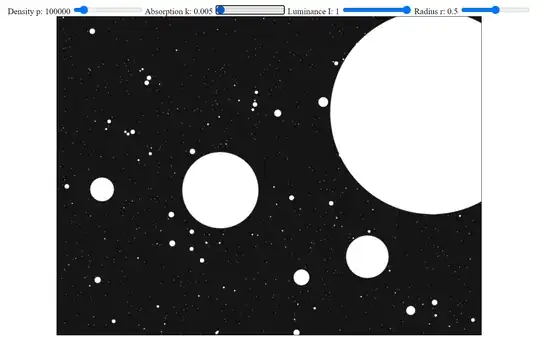
In both images, there is a perfectly bright wall of simulated stars a short, fixed distance away from the observer. Radiation from that wall leaks and is visible as a uniform grey background when the simulated wall is very close and the density of attenuating matter approaches zero, but if the wall of light is slightly more distant or the density of attenuating matter is only slightly increased, the background very rapidly approaches pitch black, despite there still being an infinite number of perfectly bright stars intersecting every possible line of sight.
You can bump up the stellar density, radii and luminosity as high as you want, and even a tiny percentage of non-luminous matter still overwhelms the resultant apparent brightness calculations with the exponential decay induced by material attenuation.
Of course arguments about thermodynamics I often see cropping up around this subject are just begging the question. How nonluminous matter is able to be there and coexist with stars is a separate matter of discussion. (How stars got there is too, come to think of it). The fact that it is there and that we know it is there, even at great distances, disproves the idea that Olbers's paradox is a paradox at all, as it completely fails to falsify an infinite and uniform universe given what we know. If one demands thermal equilibrium as a consequence of the "static universe" claim, then stars would not exist, invalidating the most basic premise of the thought experiment. But stars do exist, and so does interstellar matter. Therefore observationally, a humble law of 18th-century optics actually provides a perfectly satisfactory model that fully explains the dark night sky even with an infinite universe filled with a uniform density of stars. It also predicts uniform, low-wavelength cosmic background radiation.
In case someone thinks this idea is absurd, that even a small amount of matter between stars can block nearly all of the light from them, remember that despite how brightly the Sun shines at noonday and how close it is to the Earth, you can block almost all of that light using a thin cardboard cereal box or a parasol consisting of cloth a couple millimeters thick. This gives you an idea of how effective exponential attenuation is. Can there not be the equivalent matter of one millimeter of cardboard between you and a star 3 billion light years away, among the dust, the stellar remnants, the comets, the hypothesized Oort-like clouds, the planets, the gas clouds, etc.? If not, then what are stars (and their systems) made of?
So no, Olbers' Paradox is not really a paradox at all as soon as we updated it with 1930s observational astronomy and do the math based on what we have observed, that there is indeed non-luminous matter between ourselves and distant stars, and it has an exponential decay effect.
The infinite extent and uniform distribution of stars throughout the universe remains completely unfalsified.
Eat your heart out, Orson Pratt.




