Why does the Dopfer EPR experiment require coincidence counting?

Question

Dopfer Momentum-EPR experiment (1998) seems to provide a interesting tweak in the EPR experiment.

To read more details on this experiment, see:

• Page 3 (labelled S290) of 'Experiment and the foundations of quantum physics' by Anton Zeilinger

• Slide 11 of these slides by John G. Cramer:

• A discussion of the experiment, the coincidence counter, and how the conditions of the no-signaling theorems might not apply to this setup in the vixra paper 'Is Faster Than Light Communication Possible?' by Raymond W. Jensen.

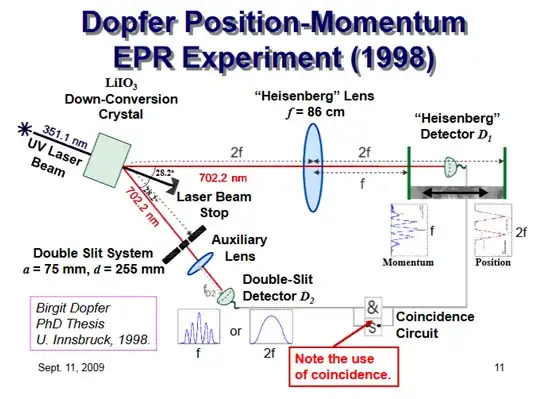
In summary, the experiment sends two entangled photons A and B toward two separate arms. Arm A has a lens and a Heisenberg detector, which can be placed either at the focal plane or the image plane. Arm B is sent on a two-slit filter. The observed results of this experiment are as follows:

1) if the Heisenberg detector at arm A is placed at the focal plane, the output of the two-slit filter at arm B is an interference pattern

2) if the Heisenberg detector at arm A is placed at the image plane (twice the focal plane) the output of the two-slit filter at arm B is an incoherent sum of intensities from each slit

As suggested in the 3rd paper link I posted, if you use time bins, there really doesn't seem to be any need at all to rely on the coincidence counter, as you can study the interference pattern on each time bin in isolation from photons received in other time bins

Am I confused? How is the coincidence count being used at all? notice that the interference pattern is spatial, not temporal!

Answer 1

1) if the Heisenberg detector at arm A is placed at the focal plane, the output of the two-slit filter at arm B is an interference pattern

That's neglecting an important point:
if the detector at arm A is placed at the focal plane then it is placed/sensitive only to a small region (or idealized: "only at one point") of the focal plane,
while (more or less) the entire focal plane of arm A is being illuminated during the experiment.

The coincidence condition therefore selects one particular pattern among all ("idler") signals detectable at arm B,
which otherwise, overall (without any selection) sums up to the "envelope shape" (or "incoherent sum").

Edit -- Note relating to comments:

An equivalent description of the dependencies between detectors A and B due to the coincidence selections is the "Klyshko relation", D.N. Klyshko, Sov. Phys. JETP 67, 1131 (1988), to which B. Dopfer referred in her thesis (german).

Roughly, as far as I understand it and relied on it for commenting:

The detected events at B that remain after coincidence selection wrt. events detected at A are "just as if" detector A were replaced by a light source (and the LiO₃ crystal were replaced by a suitable aligned mirror); and vice versa:
the detected events at A that remain after coincidence selection wrt. events detected at B are "just as if" detector B were replaced by a light source (and the mirror is suitably placed).

This equivalence can surely fail if detectors A or B were moving too rapidly. Therefore a condition for it being a useful description is that one of the detectors remains fixed while the other is moving only slowly, or in discrete steps, when scanning some region; which seems well satisfied in the Dopfer experiment.

Answer 2

If any "timing" (or coincidence) is disregarded, i.e. if simply every photon detected in arm B is considered, then there's no interference pattern obtained at all, but always only the "envelope shape"

What he means is if you disregard coincidence, you will get excess noise from singles (and doubles where the twin is undetected), which will drown out the interference pattern. You can use this kind of argument against practically any FTL scheme. So the question is, why bother coming up with a "no-signaling theorem" in the first place?

One answer to this is that the argument that any FTL signal will be drowned out by noise is insufficient. For example, you can filter out the noise due to singles in the Dopfer experiment by using a three-photon GHZ state. The one behind the 2-slit observing the interference pattern (or none) will receive 2 photons of the trio, the third one going to the Heisenberg Detector--D1 in fig.4.6. The only noise will be from "receiver-only" doubles as well as triples where the opposite of the trio never reaches D1.

When I first saw this experiment in Zeilinger, Rev. Mod. Phys. 71, 1999, p.S288 the thought that it might be used for FTL signalling was immediately obvious. Apparently R. Srikanth had the same idea (you can look him up in arxiv). But the experiment is difficult to model. It is much simpler to model Aspect/Grangier/Rogers 1986 (in Europhyiscs Lett. 1, p.173) setup using an entangled state and a Mach-Zehnder interferometer, and modify it so that the 2nd photon used in coincidence, which does not go through the MZ, can either simply be measured (like done in the experiment) or, together with a beam splitter and a second detector, have it's which-way information determined, in the MZ plane. Doing things the latter way obviously will destroy the interference pattern that Aspect observed. I wrote an article on this in 2004--see Space Technology & Applications International Forum - 2006, M. El-Genk, ed. , pp. 1409–1414.