My post is an elaboration of those here and here.
In my AP Physics C class, I was introduced to the following equation for center of mass (CM): $$x_\text{cm} = \frac 1M \int x\, dm.$$ Above, $dm$ represents a "slice" of the given object.
Problems would then be solved using the below format:
Prompt: "Find the CM of a metal rod with constant density, mass $M$, and length $L$."
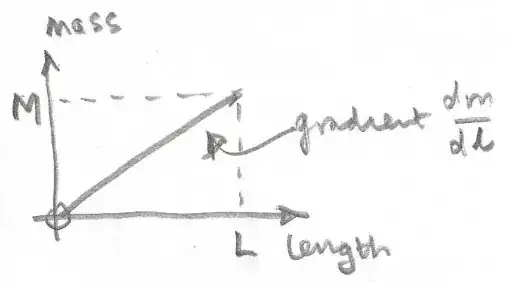
Observe that $M/L = dm/dx$ so $dm = \frac{M}{L}\, dx$. Then: $$\begin{align*}x_\text{cm} &= \frac 1M \int x \, dm \\ &= \frac 1M \int \frac ML x\, dx \\ &= \int^L_0 \frac{x}{L} \tag 1 \\ &= \frac{L}{2}\end{align*}$$ The boundaries of integrations at (1) appear since the object ranges from $x = 0$ and $x = L$. They are not specified in the formula though because we don't necessarily integrate over $x$. For more examples of this form of problem-solving, see Dan Fullterton's video.
I am confused by the statement:
"Observe that $M/L = dm/dx$ so $dm = \frac{M}{L}\, dx$."
Manipulation of $dx$ and $dm$ is mathematically undefined since infinitesimals aren't variables.
Since I couldn't understand the class-provided technique, I ended up employing the equation below for an object spanning $x = a$ to $x = b$: $$x_\text{cm} = \frac 1M \int^a_b \lambda(x) x\, dx.$$ Above, $\lambda(x) = \rho (x) \cdot A(x)$ where $\rho(x)$ provides the average density at the object's intersection with the plane at $x$, and $A(x)$ is the area of that intersection.
Is this a valid alternative equation? Also, how does the earlier technique work in a technical sense?