Potential vs Kinetic Energy of Particles in Gas

Question

"In the gas phase, the molecules are freely moving particles traveling through space, where the kinetic energy associated with each particle is greater than the potential energy of intermolecular forces."

Qualitatively, this makes perfect sense. The particles have are moving very quickly which trumps any attractive forces.

However, I don't quite understand the energetics of such a situation. This motion is where the kinetic energy term comes from. On the other hand, the tendency for the particles to attract is represented by a potential energy term. Two particles that are attracted to one another in close proximity would have a positive potential energy, right? How do we know that the kinetic energy term has to be greater than the potential energy term?

EDIT IN RESPONSE TO ANSWER

Thought I would post this in case anyone else was confused. This is my rationalization of the answer.

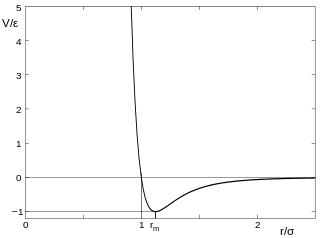
This has cleared up a lot for me. This also has to be why solids vibrate in place. For the following, assume two particles in one dimension. Assume the particles are at some finite distance from each other, each with no KE. Call this distance d. We can define the PE to be 0 at this distance, d. Since they attract each other, they fall towards one another. The attractive force is applied across the distance between them, hence work. The amount of work (or force * dist) to bring the particle to a certain velocity is its kinetic energy. In other words, all of the PE is converted to KE. Assuming the particles then “collide,” elastically of course, the particles reverse directions. They are now moving away, each with some KE. They still attract one another, however. The attractive force will apply itself across some distance. Well the amount of work to stop them will be equal to their KEs. This will happen at a distance at the distance d. At this point, there will not be enough KE to keep moving away from one another. They fall back towards one another and the process repeats. This is the vibration. In a gas, there is not enough attraction to stop the moving away from one another. In other words, the KE outweighs the PE.

Answer 1

A correction, the potential describing the inter-molecular force is negative. Have a look at http://en.wikipedia.org/wiki/Lennard-Jones_potential. If both molecules have a separation distance that puts them between 1 and 2 on the horizontal axis of the attached figure ,that means their potential energy is negative. Hence their total energy is

:

Total energy = kinetic energy (positive by definition) + potential energy (sign depends on the sign of the potential)

So if they are between 1 and 2 on the horizontal axis in the attached figure, the previous addition will become subtraction. In order to make the molecules free their total energy has to be positive which means their kinetic energy has to exceed their potential energy.

Answer 2

The kinetic energy of the gas molecules is higher than that of attractive forces or intermolecular attraction (speaking in terms of physics). In these cases, the molecules are set in motion.

Answer 3

I'm using the same potential energy diagram to describe the energetics of gases.

- The diagram can roughly be divided into 3 regions. On the right side shows the (average) potential energy of a gas which is always slightly negative. This is when gas molecules are far apart (large $r / \sigma$) and the gas state rules. The (average) kinetic energy dominates and total energy is definitely positive.
- When gas molecules get close enough as shown in the middle region of the diagram, the potential energy gets negative enough to cancel 100% of kinetic energy (which is always positive) and more, the total energy becomes negative. As a result, the gas can no longer exist because it condenses to liquid or solid.
- So, what happens to the left side of the potential energy diagram, where PE is overwhelmingly positive? That part of diagram is only used for understanding (or maybe for some extreme cases). For our usual world, matter (gas, liguid or solid) doesn't reach that part of diagram.
- As a convenience and a first approximation, gases are treated by ideal gas law. Then the PE term is totally dropped. PE diagram is not used. Under this approximation, KE is the only term. KE totally decides the temperature of the gas. This is called Dalton's atomic theory of gases.
Hope these help.