I am not completely sure I understand why you think there is a contradiction between the periodic boundary conditions and the fact that the wavefunction picks up an Aharonov-Bohm phase factor, but I'll take a stab at it.
From the comments I gather you feel that the periodic boundary condition on the wavefunction is sufficient to impose a fundamental symmetry on the system, and that the presence of the AB phase factor contradicts this. But in fact the periodic boundary condition (combined with an expectation of continuity) are only sufficient to impose quantisation on a certain parameter that appears in the solution of the Schrödinger equation (which also implies quantisation of the energy).
In addition, note that the magnetic field lifts the two-fold degeneracy of the particle in a ring (the magnetic field/current introduces a directionality).
Instead of the case with no magnetic field anywhere, where the energy is given by $\frac{n^2 \hbar^2}{2mR^2}$, the energies are now $\frac{\hbar^2}{2mR^2}(n - \frac{q\Phi}{2\pi\hbar})^2$, where $n \in \mathbb{Z}$, and $R$ is the radius of the ring.
So even though the magnetic field at the particle is always 0 there is, in fact, a difference between the particle going 'with' or 'against' the current, and this is reflected in the distinct energy eigenvalues. Viewed in this way picking up a phase after a revolution doesn't seem so strange (although the AB effect certainly does, upon first encountering it).
Edit - 13/9/2023
I have given this more thought. Firstly, the magnetic flux isn't quantised. It would be if we were dealing with a superconducting ring, but that is a different situation.
Secondly, as you already know, a pure phase change doesn't have any physically observable effect by itself - the expectation values don't change, generally speaking.
I think the fact that this is troubling you is a pointer that you should read e.g. chapter 9.1 of Atland and Simons (as mentioned in the comments). I will attempt to summarise the relevant pieces here.
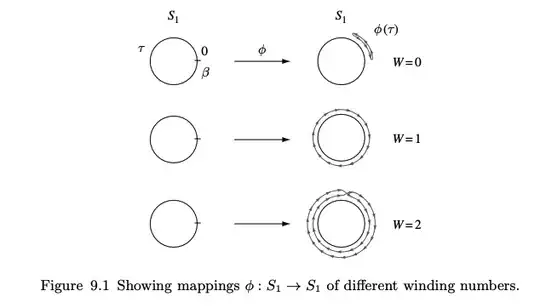
Basically, there are topological considerations at play. The $n$ that appears in the expression for the energy is a winding number. The $\phi$ parameter can be elevated to a field, such that the Lagrangian of the system is given by $L(\phi, \dot{\phi}) = \frac{1}{2} \dot{\phi}^2 - iA \dot{\phi}$. This permits a path integral formulation, where the path integral boundary condition is such that the phase is only defined up to integer multiples of $2 \pi$ (see below for screenshot from the textbook).
You can perform a gauge transformation at each angle by $\psi(\phi) \rightarrow e^{i\frac{q\Phi}{2\pi \hbar}\phi}\psi(\phi)$, so that one revolution corresponds to $e^{i\frac{q\Phi}{\hbar}}\psi(\phi)$ (the AB phase factor). This is a gauge transformation of the Schrödinger equation with the Hamiltonian of classical electrodynamics (see e.g. exercise 4.61b in the 2nd edition of Griffiths' QM book). If I have performed the correct calculation, this should change the boundary condition to $\psi(0) = e^{i\frac{q\Phi}{\hbar}}\psi(2\pi)$.
Maybe take this with a grain of salt (I welcome being corrected by someone more knowledgeable), and have a look at chapter 9.1 of Atland and Simons. You should be able to find a copy online. My apologies if this is more confusing than helpful, but I quite enjoyed reading up on the topic, so thank you for the question.
