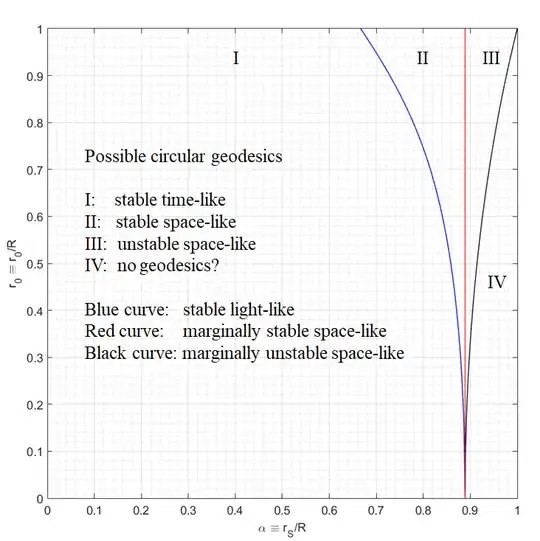
I examine parametric stability of interior Schwarzschild solution by analyzing its circular geodesics. The picture below shows the result of solving corresponding geodesics equation (Is black hole event horizon a transcendent tachyon?). Depending on combination of the reduced Schwarzschild and geodesics curvature radii, $\alpha\equiv r_S/R$ and $r_0\equiv r_0/R$, there are four distinct regions divided by three curves in the diagram.
My question is how to interpret the region $\text{IV}$? It represents the spacetime "behind" the hyperspace defined by the equation $g_{00}(r,\alpha)=0$, however there are no circular geodesics there.