0

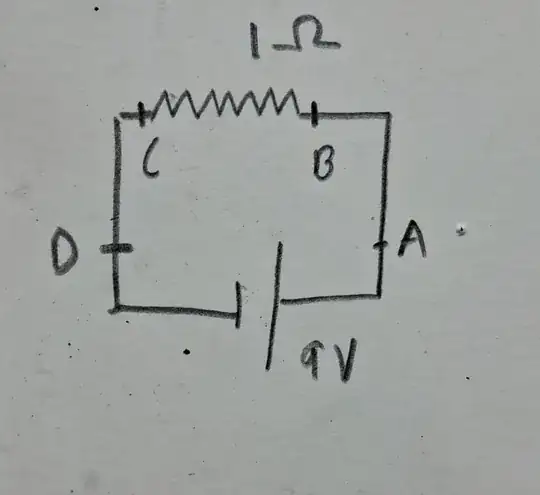
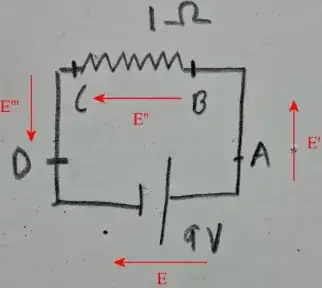
In electrostatics we were taught that Voltage drop is the work done by an electric field in bringing a unit charge from point A to point B. Or $V= E.d$ where $d$ is the displacement between A and B. Till this point, I have no problem.

Now my doubt is that in a circuit the electric field created by the terminals must be constant right? So suppose I have a circuit consisting of a 9V battery and a 1-ohm resistor.

enter image description here

Let us assume that the distance between AB and BC is equal. Since $E$ is constant and $d$ is same, shouldn't $E.d$ be the same for both AB and BC? Why do we say that $V$ across AB is 0 while that across BC is 9? Why is the resistor affecting the term $E.d$?

Qmechanic
  • 220,844
Pumpkin_Star
  • 252

3 Answers3

3

Now my doubt is that in a circuit the electric field created by the terminals must be constant right?

Not correct. The electric field is created by distributions of charges. But the conductors and the resistor consist of lots of mobile charges that can redistribute to create different fields in different situations.

It turns out that at steady state, the field in the conductor is greater in regions of greater resistance. E is not constant in the circuit.

See: Why is the electric field highest in regions of highest resistance?

BowlOfRed
  • 42,997
  • 3
  • 68
  • 123
3

Voltage drop is the difference of potential between two points, the points A and B are at same potential while the points B and C are not at the same potential, the difference in the potential

As for why this happens is interesting, in a conductor the electrons are fairly free and align them quickly to nullify the electric field, but inside a resistor the electrons has to face resistance, and due to which they are unable to nullify that and an electric field sets up in the whole resistor.

2

enter image description here

For the loop $DABCD$, $\displaystyle \oint \vec E\cdot d\vec s=0$ with the integral $\displaystyle \int_{\rm D}^{\rm A} \vec E\cdot d\vec s$ being of the opposite sign as compared with the other three integrals $\displaystyle \int_{\rm A}^{\rm B} \vec {E'}\cdot d\vec s,\,\int_{\rm B}^{\rm C} \vec {E''}\cdot d\vec s,\,\int_{\rm C}^{\rm D} \vec {E'''}\cdot d\vec s$.

The integrals $\displaystyle\int_{\rm A}^{\rm B} \vec {E'}\cdot d\vec s$ and $\displaystyle \int_{\rm D}^{\rm A} \vec {E'''}\cdot d\vec s$ usually neglected because the resistance of the connecting wires is assumed to be very much smaller than $1\Omega$ and thus $\vec {E'},\,\vec {E'''}\ll \vec {E''}$.

The electric field are set up by an accumulation of charges around the junctions between the circuit elements.

Farcher
  • 104,498