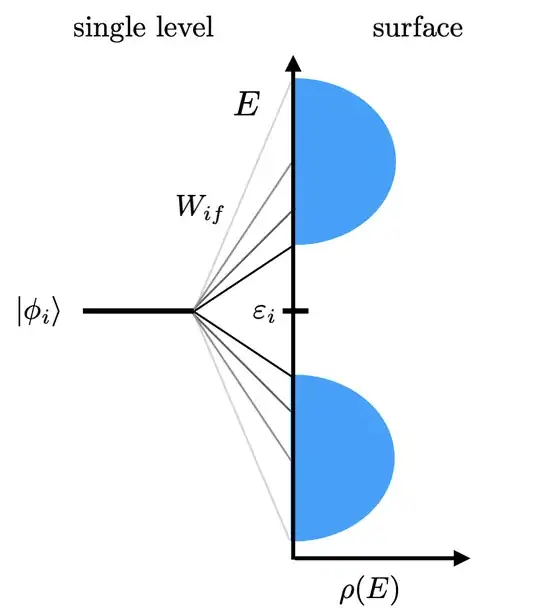
$$\lambda=\frac{2\pi}{\hbar}|V_{fi}|^2\rho(E_{f}).$$
...
Now I personally did not get the logic as to why we must incorporate this factor, and don't the same thing apply for the ground state too also.
Fermi's golden rule provides an expression for the decay rate. But maybe you also want to know where that comes from. I will use units where $\hbar=1$.
I'll start from first order time-dependent perturbation theory, and I'll elide a few of the steps for time.
In the interaction picture, to lowest order in the interaction, the state is:
$$
|\Psi\rangle = |\psi_i\rangle - i\lim_{\epsilon\to 0}\int_{-\infty}^t dt' e^{\epsilon t'}V_I(t')|\psi_i\rangle\;,
$$
where $\psi_i$ is the initial state of the non-interacting hamiltonian and $V_I(t)$ is the interaction in the interaction picture. And where I have inserted a $e^{\epsilon t}$ by hand, where $\epsilon$ is infinitesimal. The $e^{\epsilon t}$ indicates that the interaction is "turned on" in the distant past (since $e^{\epsilon t}\to 0$ as $t\to-\infty$).
Using the above expression, the transition rate for $\psi_i\to\phi_f$ is found to be:
$$
R_{if} = \lim_{\epsilon\to 0}|\langle\psi_f|V|\psi_i\rangle|^2\frac{2\epsilon e^{2\epsilon t}}{|E_i - E_f + i\epsilon|^2}\;,\tag{1}
$$
where $E_i$ and $E_f$ are the unperturbed energies of the initial and final states, respectively.
Notice however that Eq. (1) is zero unless $E_i = E_f$. Indeed, we can use the definition of the delta function to see that
$$
R_{if} = 2\pi |\langle\psi_f|V|\psi_i\rangle|^2\delta(E_i - E_f)\;.\tag{2}
$$
Eq. (2) gives the expression for the transition rate from a fixed initial state to a fixed final state. However, in most experiments we have no way to control which final state we decay into. Therefore, in most experiments we really want to know the transition rate to any final state:
$$
R_{i\to{\text{any}}}=\sum_f 2\pi |\langle\psi_f|V|\psi_i\rangle|^2\delta(E_i - E_f)
$$
Now, we use the definition of the density of (final) states $\rho_f(E)$ in energy to write
$$
R_{i\to{\text{any}}}=\int dE' \rho(E') 2\pi |\langle\psi_f|V|\psi_i\rangle|^2\delta(E_i - E')
$$
$$
=2\pi\rho(E_i)|\langle\psi_f|V|\psi_i\rangle|^2\;,
$$
where the matrix elements has been assumed to only depend on the energy and where both the initial and final states in the matrix element are evaluated at the same energy ($E_f=E_i$).
Note also, that in cases where the final state of the interacting system includes more than one particle (say the decaying particle along with a secondary particle such as a photon that carries off energy) then the density of states for the final states includes the final states of both the decaying particle and the final states of the secondary particle. And the energy must be apportioned appropriately to each final state particle.
For example, if the final state also contains a photon, then we would write the total final state as $|\psi_f\rangle = |\phi_f\rangle\otimes|\vec k_f\epsilon_f\rangle$, where the $\phi_f$ now refers to the electronic (or nuclear or whatever) state and the rest refers to the photon.
In such a case, the interaction term may be simply factorable, for example, in the case of an electron-photon interaction at lowest order:
$$
V \sim \hat{\vec p} \cdot \vec A
\sim
\sum_{\vec q}\vec \epsilon\cdot\hat{\vec p} \hat a_{\vec q}^\dagger+\text{h.c.}\;,
$$
where $\hat p$ operates on electronic state and the $\hat a$ operates on photon states.
In such a case, we can write:
$$
R_{i\to{\text{any}}}\sim\int d\omega \rho_\gamma(\omega)\int dE' \rho_{e}(E') 2\pi \epsilon_i\epsilon_j^*
\langle\phi_f|\hat p_i|\phi_i\rangle
\langle\phi_f|\hat p_j|\phi_i\rangle^*\delta(E_i - \omega - E')\;,
$$
Or, assuming we are insensitive to detecting the outgoing photon polarization, we write the spectrum as a function of photon frequency as:
$$
\frac{dR}{d\omega}\sim 2\pi\rho_e(E_i-\omega)
|\langle\phi_f| p_i|\phi_i\rangle|^2\;,
$$
where we see that the electronic (or nuclear or whatever) density of states is evaluated at the "final energy" $E_i-\omega$ due to the photon carrying away the rest of the energy.
 $cm^−1$ " />
$cm^−1$ " />