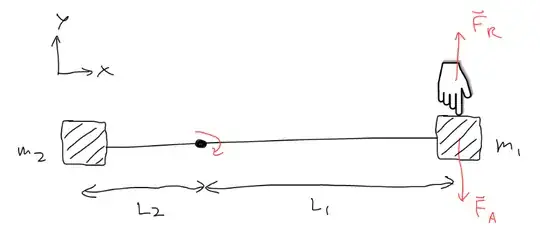
Suppose we have an ideal massless lever with a fixed pivot point and a mass $m_{1}$ (at radius $L_{1}$) on one end and mass $m_{2}$ (at radius $L_{2}$) on the opposite end, and assume gravity plays no role in the scenario. Suppose also that I apply a constant force of $F_{A}$ onto mass $m_{1}$ perpendicular to the lever. This causes the lever to rotate as indicated in the sketch below.
Of course by Newton's third law, there will be a reaction force $\vec{F}_{R} = -\vec{F}_{A}$ on my hand. Let us calculate the angular acceleration of the lever.
The applied torque on the lever is $\tau = F_{A}\cdot L_{1}$ in the clockwise direction. The moment of inertia of the entire setup is $I = m_{1}L_{1}^{2} + m_{2}L_{2}^{2}$, so the angular acceleration will be $$ \alpha = \frac{F_{A} L_{1}}{m_{1}L_{1}^{2} + m_{2}L_{2}^{2}}. $$
Now I will calculate the net force on mass $m_{2}$. Since the calculation is not as essential as the result, the reader can skip the piece quoted below.
If we take the $xy$-coordinates to be centered at the pivot with mass $m_{2}$ initially at $\vec{x}(0) = (-L_{2}, 0)$, the position of mass $m_{2}$ at later times will be $$ \vec{x}(t) = (-L_{2}\cos(\tfrac{1}{2}\alpha t^{2}), L_{2}\sin(\tfrac{1}{2}\alpha t^{2})). $$ The velocity is $$ \dot{\vec{x}}(t) = (L_{2}\alpha t \cdot \sin(\tfrac{1}{2}\alpha t^{2}), L_{2}\alpha t \cdot \cos(\tfrac{1}{2}\alpha t^{2})), $$ and the acceleration is $$ \ddot{\vec{x}}(t) = (L_{2}\alpha\sin(\tfrac{1}{2}\alpha t^{2}) + L_{2}\alpha^{2}t^{2}\cos(\tfrac{1}{2}\alpha t^{2}), L_{2}\alpha\cos(\tfrac{1}{2}\alpha t^{2}) - L_{2}\alpha^{2}t^{2}\sin(\tfrac{1}{2}\alpha t^{2})). $$ At the initial time $t=0$, we find $\ddot{\vec{x}}(0) = (0, L_{2}\alpha)$, so overall mass $m_{2}$ initially experiences a force $$ F(0) = m_{2}\cdot |\ddot{\vec{x}}(0)| = m_{2}\cdot L_{2}\alpha = \frac{m_{2} L_{1}L_{2}}{m_{1}L_{1}^{2} + m_{2}L_{2}^{2}} F_{A} $$ in the $+y$-direction.
Hence at $t=0$, the net force on $m_{2}$ is $$ \vec{F}(0) = \frac{m_{2} L_{1}L_{2}}{m_{1}L_{1}^{2} + m_{2}L_{2}^{2}} F_{A} \vec{e}_{y}. $$
Now in this scenario, what is the reaction force accompanying $\vec{F}$ and where is it applied? By Newton's third law, there must be an equal and opposite reaction force, but there is no apparent reaction force accompanying the force I calculated above.
In a previous post of mine, I questioned whether the strong form of Newton's third law holds, but now I'm confused as to how even the weak form of the law applies to this situation. Can someone clarify what is going on here?