Newton's third law states that for every force applied by object $A$ on object $B$, there is an equal an opposite force by object $B$ on object $A$. The strong form of Newton's third law states that for every force applied by object $A$ on object $B$, there is an equal an opposite force by object $B$ on object $A$, and these forces are along the line of sight between $A$ and $B$.
By the strong form of Newton's third law, we are able to derive conservation of angular momentum and many other principles of rotational mechanics.
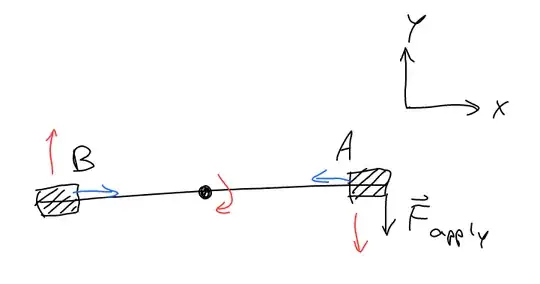
Now consider a lever with a fixed pivot with masses $A$ and $B$ on both ends. Let's say it rotates in the $xy$-plane and it is initially along the $x$-axis. To make things further clear, let's say the pivot is at the origin $x=0$, $A$ is at $x>0$, and $B$ is at $x<0$.
When I apply a force on mass $A$ in direction $-y$, the lever rotates clockwise, and mass $B$ initially moves in the $+y$ direction. During that initial motion, the acceleration vector has a nonzero $y$-component, and thus by Newton's second law there is a net force with a nonzero $y$-component.
The question is, how is this possible if every force involved is supposed to be along the line of sight between two objects/particles? Even if we consider the lever as part of our analysis, the lever itself is along the $x$-axis, so different parts along it are separated by an $x$-coordinate, not a $y$-coordinate, so no force along $y$ should ever arise.
What makes this more confusing/paradoxical is that the laws of rotational mechanics, which are used to calculate how the lever would rotate due to the force applied on $A$, are derived from the assumption that forces are only along the line of sight between two objects, and yet in the end this seems to be violated.
What I am particularly interested in is, how would we model the lever + masses scenario so that I can see exactly where the $y$-component of the force comes from? Even if we assume the lever has thickness or isn't fully rigid, it isn't clear to me how the forces act.