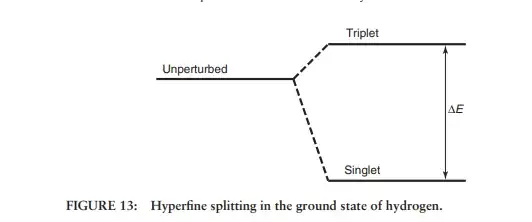
In Griffiths, the hyperfine structure is described as follows:
So the hyperfine structure is a result of a mechanism called spin-spin coupling, which is the interaction of the spin of the nucleus (proton in this case) with the spin of the electron. The spin of the nucleus has a magnetic moment which creates a magnetic field and this magnetic field creates a torque on the spin/magnetic moment of the electron. So this lifts the degeneracy in the triplet state and the singlet state.
However, when I look up another image, I get the following:
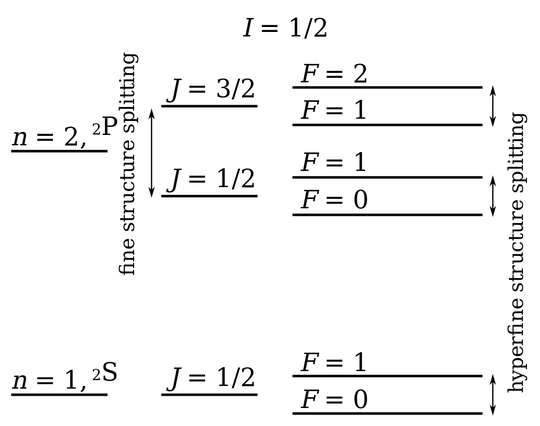
where $F = J + S$, where $J$ is the total angular momentum of the electron (spin and orbital angular momentum) and $S$ is the spin of the nucleus/proton. This lifts the degeneracy in the $m_j$ levels (if that is even a correct statement).
So my questions are:
Are these two things consistent with each other? (degeneracy in spin states vs. degeneracy in mj levels).
Is it even correct to state that hyperfine structure lifts the degeneracy in mj levels? (This is however true for the Zeeman effect), as there is a clear dependence on mj)
Is the hyperfine structure a result of the interaction between the spin of the nucleus and the spin of the electron (spin-spin coupling)? Or is it a result of the interaction between the spin of the nucleus and the total angular momentum of the electron (so spin of electron and orbital angular momentum of electron)?