7

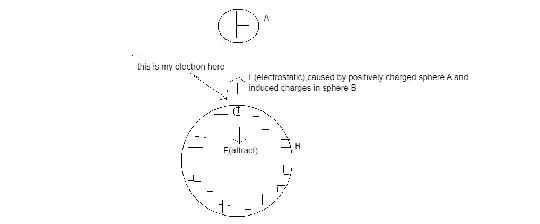
When a conductor is in electrostatic equilibrium, as far as I know, the electric field on the surface must be perpendicular to the conductor. This leads to a rather difficult problem for me, if the electrostatic force (as far as I know, this force includes the attraction of the ions + the repel of electrons) is acting on the electron's outward direction as shown, then there must be a force F (attraction) pulling it inward to satisfy the equilibrium condition and prevent electrons from leaving the conductive material. So what is this force really?

I am looking for a qualitative explanation (not a mathematical one) and on top of that. I hope someone can clarify this for me. Thank you!

enter image description here

newbieatphysics
  • 164

2 Answers2

8

As pointed out in the comments, electrons are bound in metals both by electrostatic and quantum mechanical interactions. Your intuition is correct, though: if the electric field is strong enough, the electrons will be emitted from the surface. This is called "field emission" and it happens when an electric field on the order of tens of MV/m is present. The reason why we can ordinarily treat a metal surface as a perfect "barrier" for electrons is exactly the fact that it is very hard (and unusual) to make such strong fields. Field emission in vacuum should, by the way, not be confused with gas discharges, which happen in much weaker electric fields.

FlatterMann
  • 3,155
4

A conductor consists of positively charged ions, forming a lattice, and negatively charged electrons, which are free to move within a conductor. The net charge is zero, and so the net force is actually zero.

The problem is that, according to the Earnshow's theorem, an equilibrium of a system of classical point charges is always an unstable one - that is, we would expect a metal to gradually lose its electrons and become positively charged. The reason why this doesn't happen is the exchange interaction between electrons, which is a quantum mechanical effect. There is a detailed and pedagogical calculation in Fetter&Walecka's book Quantum Theory of Many-Particle Systems.

Note also that the fact that the force is perpendicular to the conductor does not necessarily mean that it is directed outwards - it could as well be directed towards the conductor. Moreover, the claim that the force is perpendicular is based on classical electrostatics, which assumes that any tangential force would make electrons move and hence be screened by redistribution of charge - in a way, this argument already assumes that metals are stable (and a few other things.)

Roger V.
  • 68,984