Why is charge on a conductor stable?

Question

I know that charge inside a conductor should be zero and because of which all the charge of a charged conductor gets evenly distributed on its surface. But my question is:

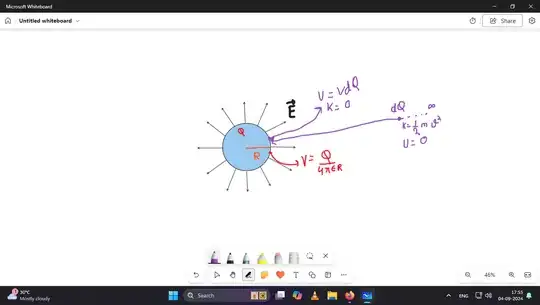
If we take a charged spherical conductor,lets say of radius$\ R$ and charge $\ Q$, the spherical conductor acts as if the total charge on it is at its center so the charge $\ Q$ develops a potential at the surface of the conductor $\ V =$ $\frac{Q}{4 \pi \epsilon_{0}R}$ where $\epsilon_{0}$ is the absolute permittivity of free space now if we want to bring a small charge $dQ$ from $\infty$ to its surface, it would have to raise its potential energy by $VdQ$ now if, at infinity if we gave it some kinetic energy that totally converts to potential energy at $\ R$, $\ K$ $\ = \frac{mv^{2}}{2}$ $\ = \frac{Q}{4 \pi \epsilon_{m}R}$ after the $\ K$ of the small charge became$\ 0$ at$\ R$ it would want to decrease its potential energy and would start accelerating in the direction of electric field which was due to the charge on the conductor and hence should leave the conductor. Why is this not the case in reality?

Answer 1

Yes that's right, for a charged conductor the electric field outside the surface is directed such as to pull charge off the surface. The reason the charge doesn't leave the surface is to do with what is going on inside the surface. There are all the interactions with the atomic nuclei and things like that. For a large enough electric field, the charge does leave the surface: that is what is happening, for example, in an electrical spark or in the flow of ions off a liquid metal ion source. For more modest fields the attraction to the atoms in the conductor is enough to prevent charge (i.e. electrons in practice) from leaving. A potential energy curve taking this into account would show a dip at the surface. In an introductory treatment this dip is often ignored and one simply asserts that some sort of other force prevents the charge from leaving. This 'other force' is the total effect of all the constituents of the conductor.