Sabine Hossenfelder says time dilation is due to acceleration in the twin's paradox. Is this true?
At 12 minutes into this video https://www.youtube.com/watch?v=ZdrZf4lQTSg, Hossenfelder states, "This is the real time dilation. It comes from acceleration."
Looking at the equations for time dilation, time dilation comes from velocity, not acceleration.
How can Hossenfelder state, "This is the real time dilation. It comes from acceleration."?
This is a matter of terminology. The term time dilation can be used in two different ways and you and Hossenfelder are using it in those two different ways.
If you are moving at velocity $v$ relative to me then your clock runs more slowly than my clock, and we can define the time dilation as:
$$ \frac{t_{me}}{t_{you}} = \frac{1}{\sqrt{1 - v^2/c^2}} $$
and I would guess this is what you are thinking of. Defined like this you are quite correct the time dilation depends only on the relative velocity $v$.
However what Hossenfelder is saying is that if you and I start at the same point and later meet at the same point then we can compare our clocks to see how much elapsed time we measured. Then time dilation means the difference in our clocks.
Now, unless we both just sat stationary in the same place the only way we can start together, separate, then meet up again is if one or both of us have accelerated. And roughly speaking the person who accelerated least measured most time on their clock. This is what Hossenfelder means by saying that acceleration causes time dilation i.e. it is the fact that one of us accelerated that caused our clocks to record different elapsed times.
If you are interested in a more rigorous explanation see What is time dilation really?, and if you're feeling really brave see What is the proper way to explain the twin paradox?
Sabine is not just wrong. She is spectacularly wrong.
Here are 5 counterexamples of Sabine's claim that time dilation and differential ageing are caused by proper acceleration.
Counterexample 4 involves neither gravity nor circular motion. Only linear motion in flat spacetime is involved, and this is the final nail in the coffin of the "acceleration causes time dilation" argument.
Counterexample 1:
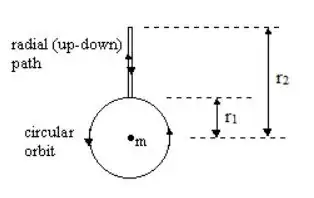
This example comes from Mathpages. One projectile goes straight up, reaches apogee and falls back down to the starting point, while another projectile orbits the gravitational body. Neither projectile is under power. Both projectiles are free-falling during the experiment, so neither projectile experiences proper acceleration, but they experience different elapsed proper times. There is no proper acceleration anywhere in this experiment to explain the differential ageing, falsifying Sabine's claim.
Counterexample 2:
One rocket hovers above a black hole using thrust to remain stationary at a Schwarzschild radius greater than $3GM/c^2$. Another rocket orbits with its engines off. They both experience the same gravitational time dilation due to having equal altitude, but the orbiting rocket experiences additional time dilation due to its orbital velocity. In this case, the orbiting rocket is in free fall, so it experiences no proper acceleration, while the hovering rocket does experience proper acceleration due to the thrust required to keep it stationary. In this case, the rocket with proper acceleration experiences less time dilation than the rocket in free fall, in direct contradiction to Sabine's claims.
Counterexample 3:
When particles are put in a centrifuge and spun up to high angular velocities, they experience extreme proper acceleration, yet all the time dilation (as measured in changes in half-life) is due to only the tangential speed, not the acceleration. This "... has been verified experimentally up to extraordinarily high accelerations, as much as $10^{18g}$ in fact. See the Clock Postulate. by Baez.
Real experiments carried out by scientists confirm that acceleration has no effect on the half-life of radioactive elements, in direct contradiction to Sabine's claims.
Counterexample 4:
A slightly modified Twin paradox. Consider the diagram below, created by DrGreg of Physicsforums.
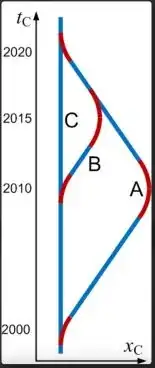
In this spacetime diagram (time up, space across), twin $\text{A}$ accelerates away from Earth and returns as in the usual Twin paradox. Twin $\text{B}$ also accelerates away from the Earth but turns around sooner, returns to Earth and waits. Both twins experience exactly the same proper acceleration for exactly the same durations. The slower ageing of twin $\text{A}$, which travels the furthest in the Earth frame, can not be attributed to a difference in proper acceleration, in direct contradiction to Sabine's claims.
Counterexample 5:
Consider two rockets following circular paths in space.
The path of rocket $\text{A}$ has a radius of $1 \ \text{light-year}$ and has a tangential velocity of $0.4c$.
Rocket $\text{B}$'s path has a radius of $16 \ \text{light-year}$ and a tangential velocity of $0.8c$.
When their locations coincide, that is the start of the experiment. After rocket $\text{B}$ has completed one revolution, it is back at the start and rocket $\text{A}$ is also simultaneously back at the start but has completed $8$ revolutions.
The relativistic equation for centripetal acceleration using units such that $c=1$ is $a = v^2/r \sqrt{1-v^2}$, where $v$ is the tangential speed as measured by an inertial observer that remains stationary at the mutual starting coordinate. The proper centripetal acceleration, as measured by the rocket pilots, is simply $a' = v^2/r$, the same as the Newtonian expectation. Rocket $\text{A}$, following the smaller circular path, experiences a proper centripetal acceleration (as measured by an onboard accelerometer) of $v^2/r = 0.4^2/1 = 0.16 \ \text{ls/s}^2$ while rocket $\text{B}$ with the greater velocity following the larger circular path experiences a proper acceleration of $v^2/R = 0.8^2/16 = 0.04 \ \text{ls/s}^2$.
Rocket $\text{B}$ experiences less proper acceleration but experiences greater time dilation, in direct contradiction to Sabine's claims.
You and Sabine are using the term 'time dilation' in different ways. I would say that Sabine is at fault here- for someone who aims to help people understand physics, she should have been more careful with her terminology.
Generally, the time interval between two events in flat space-time is 'path dependent'. If you coast directly from one event to another, the time interval will be longer than if you follow an indirect path, such as a curved or zig-zag path. The difference is a property of the geometry of spacetime. It is somewhat misleading to say that acceleration 'causes' the difference in elapsed time- it is better to say that the elapsed time is a property of the path you follow, and acceleration is just the means by which you follow a particular path.
There is a straightforward analogy with 3-D Euclidian space. The distance between two points in space depends on the path you follow from one to the other. It is shortest if you go in a straight line, and longer if you follow some zig-zag path. To follow a zig-zag path you have to accelerate, so in Sabine's terminology you might say that acceleration 'causes' the difference in path lengths- but it should be obvious to you that the length is a property of the path, and acceleration is just the means of following a particular path- acceleration doesn't 'cause' the path length to differ.
Finally, the term 'time dilation' is most commonly used to mean a special case comparing the time between two events that occur in the same place in one frame with the time between the same two events in some other frame where they occur in different places. By using the term 'time dilation' in a broader sense, Sabine is spreading confusion, in my view, as your question proves.
The answer to your question depends, of course, on what you mean by the phrase "time dilation".
I take it that "time dilation" refers to the fact that the same clock can be ticking at two different rates in two different reference frames, whereas "the twin paradox" refers to the fact that twins, present at the same place at the same time, can have two different ages.
With those definitions, time dilation is due entirely to velocity; acceleration is irrelevant. The twin paradox in special relativity is due to a combination of time dilation and acceleration. The twin paradox in general relativity, as AccidentalTaylorExpansion has explained, can be due to time dilation without acceleration.
I believe the definitions I've used are quite standard and widely used. Of course, there are always people who use language in quirky ways, and if your definition of time dilation differs from mine, then your answer to the question might differ.
In special relativity you can't compare the clocks without acceleration, but in general relativity there are examples without acceleration as well, for example on a round trip with constant velocity in a closed universe or between a twin on a circular and one on an elliptic orbit who also both experience no proper acceleration, but have different proper times everytime their paths cross.
By the way, here is a rebuttal to Sabine Hossenfelder's video in question.
While the twins are moving apart there is also time dilation. But, because they are in separate frames, these time dilations cannot be compared with each other. It is like comparing velocities in different reference frames. You think the train is going 120 km/h? Well, I think the train is going zero km/h.
While they are travelling at constant velocity they each see their other twins clock travelling at a slower rate than usual, but it is impossible to tell yet who ages more. It is only when the twins meet up that they can compare their clocks. One of the twins has aged more. How can that be? The problem is symmetric right? Each twin sees the other twin moving away, so you would expect the clocks to be equal. It turns out that one of the twins has accelerated and this has caused that twin to have aged less.
No, you can still get a "twin paradox" without acceleration.
Although some solutions attribute a crucial role to the acceleration of the travelling twin at the time of the turnaround, others note that the effect also arises if one imagines two separate travellers, one outward-going and one inward-coming, who pass each other and synchronize their clocks at the point corresponding to "turnaround" of a single traveller. In this version, physical acceleration of the travelling clock plays no direct role.
The main reason is a change in inertial reference frame, which of course can arise from an acceleration, but it does not need to.
Compare it to distances in space.
Suppose we take a journey from New York to Washington D.C. (in the U.S.A.) One route goes in a straight line. Another route goes via San Francisco (on the west coast). The second route is a lot longer. Why? Because it is longer. What else can one say?
But if you want to spot some property of the second route which gives a clue to the fact that it is longer, you can notice that it includes a change of direction (the turn-around at San Francisco). So you might say that it is longer "because" it has this change of direction. That is essentially what is going on when people focus on the acceleration part of the twin paradox.
In the spacetime case the worldline with the turn-around is the "shorter", in the sense of having less proper time, as compared with a straight worldline. The reason it has less proper time is that if you add up all the little bits of proper time along that worldline then the sum total is smaller than along the straight worldline. The straight worldline has the most proper time (between any given pair of timelike-separated events in a spacetime without curvature).
Instead of twins, think of triplets; one goes to Mars, one goes to Jupiter and one stays home. The Mars and Jupiter triplets accelerate exactly the same to the same top speed of 1/2 c, and they turn around at their planet in exactly the same manner. Any explanation that works on the basis of acceleration or of turning around would have to state that the Mars and Jupiter triplets would return and be the same age as each other. But this is simply not true. The Jupiter triplet would be younger than the Mars triplet or the Earth triplet. Special relativity time dilation is only concerned with velocity and the amount of time spent at that velocity. Acceleration or turning around has absolutely no impact on special relativity time dilation and should not be considered at all.
Physics isn't due to mathematics: it happens whether you calculate or not. The math is a story we tell about the physical phenomena. Of course, it's a very credible and effective story because we check it against reality. But in math, there is generally more than one way to tell the story. Unless the ways have different consequences for some experiment, physics can't decide which is the correct telling.
Oh, this is attracting good answers. Yukterez is giving an example from GR. AccidentalTaylorExpansion's answer is the immediately relevant one.
But I want to expand upon ATE's answer. Yes, there is no comparison if you never meet up again to compare. But to meet up, at least one of them must have accelerated (under SR). If it were completely symmetric, there will be no way to know which one of the pair should be aging. Thus acceleration is necessarily the cause of the time dilation.
However, this is still a velocity issue, not an acceleration issue. This is because you can change the importance of the velocity part v.s. the acceleration part simply by changing the wait time during the constant velocity coasting parts. This is particularly clear if you look at the Minkowski diagram---the acceleration part can be reduced to an arbitrarily small contributor, except that it is also the thing that dumps all the constant velocity accrued time dilation onto the poor twin. Which is why it is ok to study time dilation under basic SR and not have to only be considered using GR.
