I am currently running a numerical simulation for site percolation. Using periodic boundary conditions I am attempting to determine the correlation length following the method set out in this paper https://arxiv.org/pdf/1902.03708.pdf.
The Figure below shows the results of the simulation for different values of the lattice length L.
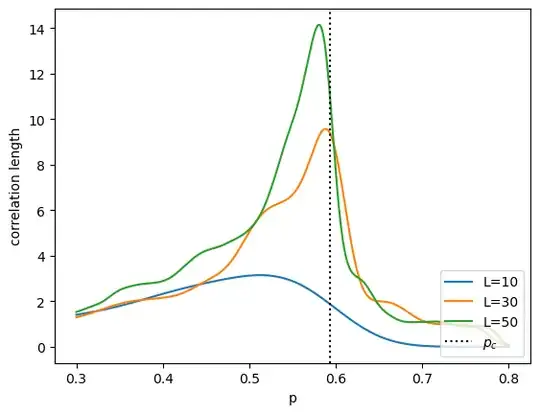
While the correlation length follows the expected shape, it seems to peak at lower values than expected. Near the percolation threshold the correlation should approach L - though this feature is not present in my simulation.
Question: Is this a feature of the correlation length for numerical simulations or is there an issue with my simulation? I.e. have I made a mistake in the program?
Edit:
This simulation is for simple site percolation on a 2D lattice. I am using the Newman-Ziff algorithm https://arxiv.org/pdf/cond-mat/0101295.pdf. The plot for the correlation length was generated from the average of 10 samples. I have also attached a visualization of the clusters at different steps in simulation for L=50.
The following definition for the correlation length is used:
$$ \xi^2 = \frac{\sum_\mu{m_\mu I_\mu}}{\sum_\mu{m_\mu^2}}$$ The sums are over all clusters (excluding the one that has percolated). $m_\mu$ is the size of cluster $\mu$ and $I_\mu$ is the moment of inertia: $$I_\mu=\sum_i^{m_\mu}(x_i-x'_\mu)^2$$ I.e. the sum of the squared differences between the cluster sites and the center of mass.
The procedure for finding the correlation length then involves tracking the moments of inertia and center of masses as the sites are added.