In Peskin&Schroeder they explain in a graphical way why the Schwinger functional generates only connected diagrams. However I don‘t understand why they get 2 diagrams since the first diagram is just a symbol for the propagator $\langle\phi(x)\phi(y)\rangle$.
The propagator has infinitely many diagrams in it, not just two. This page says that they can be categorized into ones which are connected and ones which are not. Are you getting confused with just the free propagator, which has a closed form solution?
Eq. (11.83) in P&S expresses the fact that the 2-point correlation function $$ \langle\phi(x)\phi(y)\rangle~=~\langle\phi(x)\phi(y)\rangle^c +\langle\phi(x)\rangle^c\langle\phi(y)\rangle^c,\tag{11.83}$$ decomposes into connected correlation functions. The similar decomposition for the 1-point function is $$ \langle\phi(x)\rangle~=~ \langle\phi(x)\rangle^c.$$ A proof uses the linked cluster theorem, cf. e.g. eqs. (4) and (5) in my Phys.SE answer here.
The connected 2-point function $\langle\phi(x)\phi(y)\rangle^c$ can in turn be decomposed in terms of free propagators and self-energy, cf. e.g. this Phys.SE post.
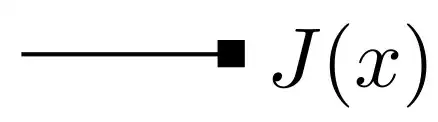
The first diagram is not a symbol for the propagator $\langle\phi(x)\phi(y)\rangle$. It is a symbol representing a sum of connected diagrams, which is indicated in the first line of Eq. (11.83). The full propagator $\langle\phi(x)\phi(y)\rangle$ is a sum of all possible diagrams (not only connected) constructed with the vertices which are generated with the Lagrangian. As Peskin&Schroder consider a theory with a source current $J$ in this section, one of the possible vertices is
Because of the presence of such a vertex, there exist disconnected diagrams which contribute into $\langle\phi(x)\phi(y)\rangle$.
The simplest diagram of such kind is
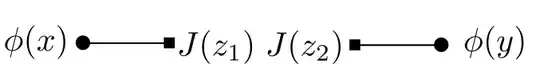Without a source current, such diagrams are usually absent.
