I've heard compelling reasons to think that it is one although why do we assert this in light of the calculation which shows a point particle creates an electrostatic field of infinite energy (see e.g. Griffiths ED 2.4.4 or Feynman Lectures vol. 2 section 28)?
Why do people not consider this calculation a definitive reason to abandon the notion that the electron is a point particle?
Why do we insist that the electron be a point particle [...]?
We do not. For example, measurements of the electron validate that it's charge distribution has spherical symmetry to within an error of $10^{-15}$. And point can't have any geometrical symmetries, hence electron is not a point particle.
Point particle approximations are used in some models for useful first order insights.
It's like when you analyze the Sun's trajectory in our galaxy: you can imagine the Sun being a "point particle", because ${d_\odot}/{r} \approx 10^{-12}\ll 1$, where $r$ is our distance to Milky Way galaxy center (about $24~\textrm{kly}$). Hence, the Sun's diameter can be ignored in these types of problems. However, in other types of problems it is important, like evaluating black body radiation, measuring the exact barycenter of solar system rotation etc.
It is the same for particles: if the model at hand doesn't require exact shape of particle, it doesn't use it.
why do we assert this in light of the calculation which shows a point particle creates an electrostatic field of infinite energy
Actually this is one of the reasons quantum mechanics had to be invented. If there were a singularity at the center of charged particles then when they were attracted to each other they would fall and neutralize so no atoms and molecules as we have measured them would exist, or us either. Bohr with his model tried to solve this by using a planetary model for bound states that has a quantized angular momentum. This eventually led to the theory of quantum mechanics and its postulates where rigorous mathematics can be used to calculate and predict the behavior of particles in the phase space region where classical electrodynamics would predict singularities.
The wave function postulate is important in this, second page in the link. The wave nature of the solution for interactions between particles, controls their behavior in interactions. Only the probability distributions of a particle being at (x,y,z,t) with four vector $(p_x,p_y,p_z,E)$ can be calculated.
See this answer of mine to get a feeling about the probability build up of the wave nature.
When we write down the equations of the Standard Model of Elementary particles, the electron appears as a field that is represented as an irreducible representation of the Lorentz group, the Dirac spinor. This is an object which has no substructure. Note that this is subtly different from a point particle, in that this is not a statement about a spatial extent. Instead, it is a statement about the field's response to Lorentz transformations (or more generally, Poincaré transformations, this includes rotations and changes in uniform velocity).
In particular, the fields are arranged in such a way that the equations of motions stay independent of a choice of inertial frame (technically, the Lagrangian is invariant under Lorentz transformations, for the free Dirac field this looks like $\mathcal{L}_\textrm{free} = \bar \psi ( i \hbar c \partial\llap{\unicode{x2215}} - m_ec^2) \psi$). This is something that in a classical setting cannot be done for an extended object. This is easy to understand if you are familiar with Lorentz contraction: e.g. a sphere will become an ellipsoid in any frame where it is moving, and thus the rotational symmetry is broken. So in classical theory, only a point-like object can be Lorentz-invariant. I believe this is why we call objects without substructure, i.e. those that transform according to irreducible representations, "point-like".
My old answer gives some insight into how the spatial "size" of such an object can be usefully defined (a radius would be the square root of the cross-sections mentioned there give or take a factor $\pi$). Now, the only reaction-independent length scale you can construct in a theory of only electrons and photons is $\frac{e^2}{m_ec^2} \approx 10^{-15}\textrm{m}$ which is known as the classical electron radius. Why is it the only one? Because there are only two inputs characterizing the theory: the electron charge $e$ and the electron mass $m_e$, and this is the only combination that has dimensions of a length. Since this is the only length scale, it is bound to appear all over the cross-sections related to electron scattering, and in that sense it can usefully be considered a measure of the size of the electron. Let me emphasize though that the actual cross-section in any reaction will also depend on the other available length scales in the reaction (derived from masses of other particles, center-of-mass energies, energy transfers ...), so one shouldn't think of the classical electron radius as "the" size of the electron.
Why do people not consider this calculation a definitive reason to abandon the notion that the electron is a point particle?
Because that calculation is based on a dubious assumption that energy associated with point charged particle is given by the standard formula for Coulomb energy of a sphere, or extended charged object with spherical symmetry. When we try radius consistent with experiments on electrons ($r<$1e-18 m), we get energy higher than rest energy of the electron. Thus the Coulomb interaction energy formula is extrapolated somewhere where it clearly does not work well.
If you allow me to paraphrase: You are making the case that since the energy of a Coulomb electric field is infinite at the origin, the electron must not really be a point particle. First I will summarize some evidence in favor of point-like particles, without coming to a final conclusion. Then I will address the Coulomb potential and our ability to make a conclusion from that infinity.
On the former: Well, really every experiment that has been done shows particle-like nature on each individual run. Let me give you some example for context.
Check out this image of the trajectory of an electron from a cloud chamber:
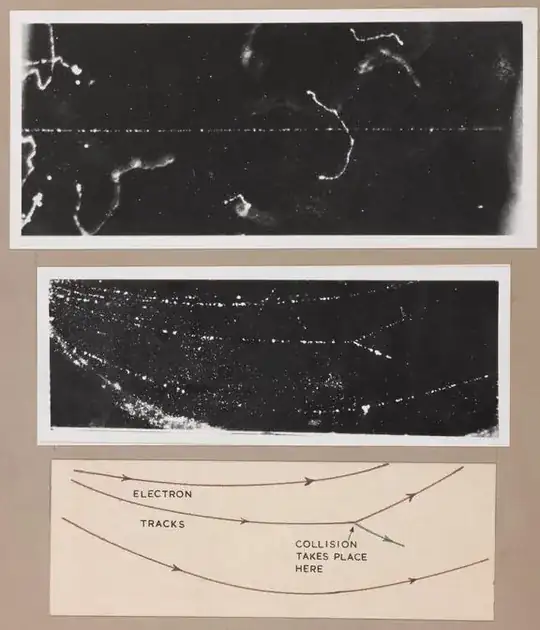
In addition, in a screen-like setup like a multi-channel plate, which is basically a bunch of cavities that an electron can enter, we only ever get a signal in one channel at once.
What else? Consider the Milikan's oil drop experiment. There's a good video of it here. The charge of the electron was found in this experiment, and every charge seen in the experiment is a multiple of that base charge. That suggests a final granularity of electrons.
There are pretty much endless other examples.
However, as we know, there is a wave nature of the electron as well. This wave-particle "duality" has confused mankind for more than 100 years and we still don't have it all quite cleanly sorted out today. Thus many of the arguments around measurement in Quantum Mechanics.
Finally I would like to add that while some experiments are suggestive of pointlike particles, this does not have to be the final say in nature. I show these experiments only to present some relevant evidence that can be weighed in.
So, how are these compatible with the infinite energy of a Coulomb potential?
The infinite energy of a Coulomb potential is an issue for sure. But we already know that our electrodynamics is not the final story, so an issue there is likely just indication of the limitations of our theory. Quantum Electrodynamics is a more fundamental theory, however even here the singularity still causes issues. We are able to tame these issues with a process called renormalization.
But regardless of whether one considers this an issue in QED... even QED is not the end of the story. Since we don't have a final theory, we don't know what an electron actually IS. So we can't rule out the possibility that there is a way for it to have a point-like nature while still having a total energy that doesn't cause our theories to blow up. The way of calculating energy (if there even is one in a hypothetical final theory) may be completely different than $\int\vec{E}^2 dV$. As such, we have no way of ruling out a pointlike nature of the electron.
An interesting point. I’ve had similar problems with the origins and properties of the electron. And they also indicate that the concept of the electron as a point particle with only neg charge should be questioned. My research shows that in 1897 Zeeman noticed spectral splitting of atomic emission lines.Lorentz explained this as proof of existence of the electron as a point particle ,proof of Lorentz force and validation of his model of electromagnetism. Yet in fact in his theory, his ion ( That’s what he called the electron initially) emits polarised radiation perpendicular to its plane of Rotation. Clearly violating all observations of induction and emission of emr up till that point. ( emr waves can only be emitted parallel to the rotation plane of a dipole). What seems to happen is Lorentz, ignored all empirical observation current to 1897 and erroneously assumes his ion /electron is a point particle with a neg charge. So my answer to,your question is Yes, people should abandon this concept of the electron as a point particle. And the reason is that its properties contradict all known observations of emr.
