Let me answer my own question; after sleeping on it, I was able to recall/remember (fragments of) arguments presented in textbooks and articles. The below is my best attempt to reconstruct those arguments from memory (I do not recall which book or article would have the most detailed argument). The below is as error-free, correct and concise as I can make it. If there are specific mistakes, vague spots or excessive hand-waving, please point these out & I will attempt to make appropriate corrections.
The goal is to show how non-relativistic semi-classical electrodynamics arises as the many-body limit of QED, for N soft photons, for large N>>1. The answer is very long, and splits into three parts. The first part is just a reminder that macroscopic structures, such as coils of wire or capacitors, can be described as sums or integrals over charge distributions or currents. This first part is purely classical and conventional physics. The second part is a short reminder/review that the Fourier transform of the Feynman photon propagator is just the Coulomb potential. That is, the exchange of a single photon can be thought of as a single interaction with a single charge (whether in momentum space or position space). The third part is the most difficult (and the most vaguely presented). It attempts to bridge between the first part (the classical many-body sum-over-charges) and the second part (the photon interactions) to show how the semi-classical (quantized to first order in h-bar) path integrals arise. It also attempts to show how the main contribution to the path integral arises from many soft photons (as opposed to the scattering from a few hard photons). This follows because the semi-classical paths are all close to the (single) classical (geodesic) path of a charge in an electric field.
The answer does not articulate the algebra of vector fields, nor how they transform under (special or general) relativity. That info is widely available, and repeating it here would be a distraction. Adding this articulation would show that the results still hold for electric currents, possibly time-varying, as well as charges.
Consider a uniform electric field, between the plates of a capacitor. The goal is, in the end, to relate this to the interaction term $-ie\,\overline\psi A_\mu\psi$ appearing in a Lagrangian. The capacitor can be approximated with a large collection of electric charges $q_n$ distributed uniformly (spatially) across the plates of the capacitor. These may be taken as fundamental charges $\pm e$. Each such charge has position $\vec x_n$, with a surrounding Coulomb field. Thus, between the plates, we may write an electric field at point $\vec y$ as
$$\vec E(\vec y)=\sum_n \frac{q_n (\vec x_n -\vec y)}{|\vec x_n -\vec y|^3} $$
I write cubed in the denominator, only so as to make the numerator be a unit vector; otherwise, this is just the inverse-square law. A limit of taking the number of electric charges $N\to\infty$ is taken later. Equivalently, the above could have been written as an integral over a charge density $\rho(\vec x)$, instead of a sum over charges.
Now, the interaction Lagrangian has an $A_\mu$ in it, so we want the an expression for the potential, and not the electric field. This is, again, textbook-standard. Writing $A_\mu=(\varphi,\vec A)$ and $\vec E= -\vec\nabla\varphi$, one has
$$\varphi(\vec y)= \sum_n \frac{q_n}{|\vec x_n -\vec y|}$$ (1)
A different expression, but working along the same lines, can be given for the magnetic field around a current flowing along a wire (or a solenoid, as desired).
By convention, quantum field theory is done with momenta (as QFT is geared for scattering); positions are eschewed, and so formalities require the Fourier transform of the above to be taken. The Fourier transform of the Coulomb potential is
$$ \frac{1}{|\vec x - \vec y|} = \frac {1}{(2\pi)^4} \int e^{-i\vec k \cdot (\vec x-\vec y)} 2\pi\delta(E)\frac{1}{k^2 \pm i\epsilon} d^3k\, dE$$ (2)
so that on the right, the conventional Feynman propagator begins to appear before our eyes. I've dropped the $\sum_n$ and the $q_n$, as carrying this about becomes an uninteresting burden. I have inserted a factor of $2\pi\delta(E)$ and then promptly integrated over it, because, once one gets to the QFT point of view, this gets interpreted as a "photon of zero energy".
The shape of the answer to the main question begins to emerge, here: the "bath of photons". This can be interpreted in one of two ways. One way is to recognize the integral as running over an infinite number of photons of momenta distributed in a certain way. These are, however, a coherent collection of photons, because the phase matters: the phase in the integral is what makes it a Fourier transform. When this gets (eventually) drawn as a wavey line in a Feynman line, it is a single line, and so is called "a single photon", albeit integrated over all momenta.
One can get the "thermal bath of photons" by interpreting the sum $\sum_n$ over the charges $q_n$ as providing that: each charge supplies one photon each; these are incoherent in the sum, uncorrelated in terms of phase. It resembles a mixed state, as will becomes more clear below. But it is still a bit early to be re-interpreting these formulas as photons, so lets put these ideas on hold.
QFT is conventionally expressed in terms of scattering states of fixed incoming and outgoing momenta, as S-matrix expressions. Another answer, by Andrew Christensen, to this posting provides the necessary details. Writing the Coulomb potential as $V(r)$ and taking it's Fourier transform as $V(k)$ one can take the scattering matrix elements as
$$ (2\pi)^4\; \langle p\, E|V(k)| p^\prime\, E^\prime\rangle = V(k)\; (2\pi)^3\delta^3(p-p^\prime-k)\; 2\pi \delta(E-E^\prime)$$ (3)
Now, eqn (1) and eqn (2) can be plugged into (3) to get an expression for the multi-photon S-matrix expression for "what is it like to send an electron of momentum $p$ in between the two plates of a charged capacitor?". That is, to obtain
$$ \langle p\, E|\int \varphi(\vec y) d^3y\;| p^\prime\, E^\prime\rangle $$
The actual plugging-and-chugging of this is a bit tedious, so I will skip it. it is more or less straight-forward; one must keep various factors and signs straight, that's all.
Now for the funny part: nothing above has been actually "quantum" in any way. The notation is suggestive, with the bra-ket notation reminiscent of S-matrix notation, and the $1/(k^2\pm i\epsilon)$ recognizable as the Feynman propagator for a photon. But all manipulations are classical, and its still a stretch to imagine "a bath of photons" in the above.
To get to "quantum", one instead starts with the QFT vacuum state $|0\rangle$. A single-photon state can be obtained by applying a raising operator to it: $|1\rangle = a^\dagger|0\rangle$ To maintain contact with scattering, momenta should be attached, and so one writes
$$| \vec k\rangle = a^\dagger_{\vec k} |0\rangle$$
as a single photon state. To get to the multi-photon state, one has to insert the raising operator $a^\dagger$ into eqn (1) and (2) to now get operator equations that correspond to an electrostatic field for a charged capacitor. The sum over charges $\sum_n q_n$ becomes a product. Again, this involves more painful plugging-and-chugging.
To make it clear what the final result is, it is easiest to write it as a Feynman diagram, which is, of course, the whole point of these diagrams: to avoid the pain of writing the long integral expressions. The diagram is obviously at tree-level, and it is manifestly multi-photon.
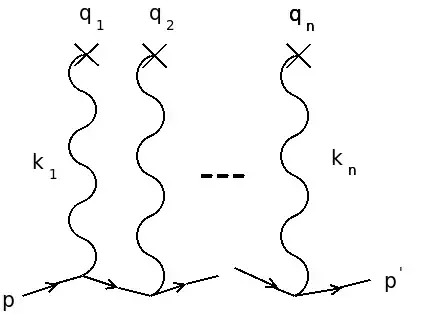
The crosses labelled $q_n$ are meant to represent the (stationary, uniformly distributed) charges in the capacitor. The wavey lines are meant to represent the photon propagators, in momentum form, here labelled with momentum $k_n$. These momenta are meant to be integrated over, with each integral giving the Coulomb potential (the cross). Along the bottom runs the electron, with incoming momentum $p$ and outgoing momentum $p^\prime$. At each photon-electron vertex, there is to be a factor of $(2\pi)^4\delta(p^\prime-p^{\prime\prime}-k_n)$ indicating conservation of momentum (and energy) at that vertex. The total diagram is meant to be a product of such vertexes, that is, a product of integrals. Viewed as an operator equation, this becomes a product of raising operators, so that the electric field is represented by many photons, and is written as
$$ |\varphi(\vec y)\rangle = \int\int\cdots\int \frac{e^{ik_1(x_1-y)}}{k_1^2+i\epsilon}dk_1 \cdots \frac{e^{ik_n(x_n-y)}}{k_n^2+i\epsilon} dk_n a^\dagger_{k_1} a^\dagger_{k_2}\cdots a^\dagger_{k_n}|0\rangle$$ (4)
where I'm sure I dropped some factors of $2\pi$ and $-i$ in the product integral above, as well as the assorted delta functions $\delta (p^\prime-p^{\prime\prime}-k_n)$ to balance the momentum, and also the electron propagators! Its a big messy expression! The integrals must be taken over all possible permutations of the charges; that is, there is no set order in which the electron interacts with the various charges.
The most interesting part of the above is not Fourier transforms, and is certainly not the horrible traces over the gamma matrices in the electron propagators, trying to account for the photon polarizations. Important, to be sure, and quite messy algebra. No, the most interesting part is the sequence of delta functions joining together the momenta. These must be arranged in such a way that the incoming electron, with the non-relativistic incoming momentum $p$ must alter its flight-path a little bit, bending, to leave with another (non-relativistic) momentum $p^\prime$. I say "non-relativistic", because one wants to encounter classical electrodynamics, here, with mass $m\gg|p|$. These delta functions (and propagators) must be arranged so that each transfers only a tiny amount of momentum to the electron, and thus they are "soft" or "infrared" photons. Since this is a product of these integrals, each of these contributing charges, a photon each, do so on a "thermal" or "incoherent" fashion. The delta functions prevent any phase from being carried from one integral to the next; the delta functions "erase" any phase dependencies between the individual photons. There is no coherence condition between them (even though, for any one individual charge, the phase is centrally important for giving the correct Fourier transform, for that one individual charge.)
What I have not done, above, but would like to do, is to demonstrate that the integral has a local maximum when all of the photons are soft. This requires writing the integrals in a form where one can use the method of steepest descent, or the multi-dimensional stationary phase method. This is the real place where the "rubber hits the road", where one gets to see the semi-classical ideas take root.
But this is too hard, and requires another three pages of writing. It can be done, as follows: one consider the classical trajectory of an electron in an electric field, and writes this as a geodesic, solving the Hamilton-Jacobi equations. This geodesic is the one that provides the extremum of the action (by definition, as solutions to the Hamilton-Jacobi eqns provide the extrema of the action) This extremum is the thing that is "stationary" in the method of stationary-phase. The goal is then to show that the rest of the multi-integral (4) is "close to" the classical geodesic. That is, the integral (4) is a vast collection of paths, but, of all of these, the only ones that contribute significantly are the ones involving "soft photons". What's more, the "physical" paths that correspond to soft photons should be "close to" the classical geodesic.
This can be done as follows: every geodesic has an accompanying "Jacobi field", which, roughly speaking, describes what directions are locally orthogonal to the geodesic, as well as providing a sense of the distance in those normal directions. The task is then to take the fourier transform of those Jacobi fields, and then to write it in such a way as to notice that a gently curving geodesic only has fourier components with very low momentum. The sum over all nearby-paths to the geodesic then contains only the "soft momenta", and discretizing this should give the "soft photons" of eqn (4) and the tree-level Feynman diagram above.
This is the hard part of answering this question, and sadly, I must leave it blank, for now. It requires too much heavy lifting in Riemannian geometry (to write the Jacobi fields for an electron gently flying through a static electric field) and too much differential geometry (to write the Fourier components, and then equate those to the multi-photon Feynmann integral.) Still, even a simplified exhibition of this would be nice.
Time for one more formula. One has the path integral
$$ Z[J] = \int [d\varphi] \exp \left(\frac{-i}{\hbar} \int d^4x \mathcal{L}(\varphi,\dot\varphi) + \varphi J \right) $$
In this expression, the $J$ is the "current", coupling to the photon field $\varphi$. To get the capacitor problem, one generates the Feynman diagram
$$ \frac{\delta}{\delta J_1} \frac{\delta}{\delta J_2} \cdots \frac{\delta}{\delta J_n} Z[J] $$
for each $J_n$ corresponding to charge $q_n$ located at $x_n$. This is an n-point, n-legged Feynman diagram; it is exactly the diagram shown above.
The Lagrangian is for the charged particle flying between the capacitor plates. The classical path of this particle is the geodesic. The path integral above is to be solved by the method of stationary phase, showing that the only paths making a significant contribution are the ones that are literally, physically nearby, close to the classical path. For them to be nearby, all bends and curvatures must be small (imagine a tube of nearby paths.) Since these are small, the corresponding momentum components are also small. Writing down "all possible nearby paths" is a big mess, but doable, using the Jacobi field. Re-arranging terms, the goal is to show that the resulting expression is exactly nothing other than eqn (4), which is the same thing as the Feynman diagram above. Phew.
In a certain very important sense, this is the answer to this question, and it is the central answer, and yet sadly, I cannot (yet) write it in the detail it deserves. The formulas (1)-(4) above only lay the basic groundwork, only provide the actual introduction to the problem to be solved. The part of the derivation that shows that the soft photons are the only ones contributing to the path integral, that part is still missing.
This answer is long, and also (as noted) incomplete. Earlier answers, and answers to other questions seem to miss entirely the point of the "bath of photons", and seem to miss the point that one must show, at the tree level, that this bath of photons is equivalent to the semi-classical path integral of the action. That is, that there is a tube of paths close to the classical geodesic, the tube is given by the Jacobi fields, and that the paths in this tube all have soft curvatures. That soft curvatures are low-momentum, and are given precisely, exactly (no hand-waving, this time) the soft photons in the integral of eqn (4).
Note/Caution: the classical path of a point charge flying through an electric field is a geodesic, and is understood easily enough. The bundle of nearby paths, contributing to the path integral, should not be thought of as (probabilistic) paths of charges, but rather as paths that contribute to the probability amplitude (and not the probability). The paths must be summed "coherently", in the sense that the relative phases of two paths matter. Worded more formally, they produce not a measure on a (weak) topology, but the square-root of that measure (including a complex phase).