This problem can be solved by reasoning, as in the other answers, or by too much math, as in this answer.
The full 3D potential due to a ring of mass or charge cannot be expressed in elementary functions. (Ciftja Babineaux & Hafeez 2006) gives the solution for the potential
$$V(\rho,z)=\frac{4G\lambda R}{\sqrt{(\rho+R)^2+z^2}}K\left(\frac{4\rho R}{(\rho+R)^2+z^2}\right)$$
where $\lambda$ is the mass per unit length (I translated from charge to mass, the result is identical), $R$ is the ring radius and $\rho,z$ cylindrical coordinates. $K$ is the complete elliptic integral of the first kind
$$K(m)=\int_0^{\pi/2}\frac{d\theta}{\sqrt{1-m\sin^2(\theta)}}.$$
To get the force we "just" need to calculate the gradient of the potential. The derivative of the integral is:
$$K'(m)=\frac{E(m)}{m(1-m^2)}-\frac{K(m)}{m}.$$ (E is the complete elliptic integral of the second kind.) Good news, we can in principle calculate the $\rho$ and $z$ derivatives. The bad news is that calculating this turns into reams of algebra. The good news is that this is what computer algebra systems are good at. I am not going to try to reproduce it here (life is too short to keep track of nested parentheses and square roots in LaTeX), but the key thing is that it is clearly nonzero in general.
Addendum: (Escalante 2021) actually works out the field explicitly. They find the slightly neater (but still messy):
$$F_\rho = \frac{G\lambda}{R}\frac{1}{\rho \sqrt{(1+\rho)^2+z^2}((\rho-1)^2+z^2)}\left\{ (\rho^2-1-z^2)E\left[\frac{4\rho}{(1+\rho)^2+z^2}\right] +((1-\rho)^2+z^2)K\left[\frac{4\rho}{(1+\rho)^2+z^2}\right] \right\}$$
and
$$F_z = \frac{G\lambda}{R} \frac{2z}{\sqrt{(1+\rho)^2+z^2}((\rho-1)^2+z^2)}E\left[\frac{4\rho}{(1+\rho)^2+z^2}\right].$$ (Here $\rho$ has been scaled so the ring has radius 1).
Since $|F_z|>0$ everywhere except for $z=0$ we can conclude that there will be a net force everywhere above and below the ring. For $z=0$ $F_\rho$ is nonzero, with a sign change at the ring $\rho=1$.
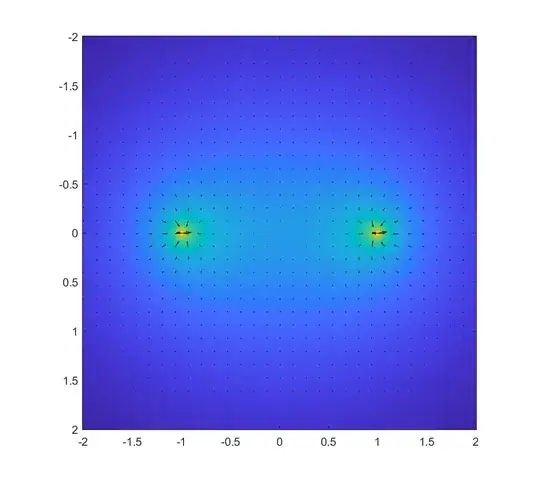
A numerical calculation also bears this out, as shown in the figure above showing the potential and gradient in a cross section of the ring. The field strength inside the ring is small, but nonzero.
Indeed, calculating the force along the z-axis (a much easier exercise) is enough to show that it is nonzero except for at the center of the ring.