0

There are YouTube videos where a person hold a cup of $\rm CO_2$ and pour it on top of burning candles to distinguish them. As far as I know, $\rm CO_2$ and $\rm O_2$ both are almost perfect ideal gas at atmospheric conditions, so the volume they occupy shouldn't affect each other. Their joint probability distribution should just be the two Boltzmann distributions in product, and should be mostly uncorrelated. If so, how can $\rm CO_2$ displace $\rm O_2$ and distinguish fire?

While a cup of CO2 has partial pressure much higher than CO2 partial pressure in the atmosphere, I feel it should still be nearly ideal since N2 is nearly ideal even though the atmosphere is almost all N2 (same order of magnitude)

Qmechanic
  • 220,844
Bohan Xu
  • 728

4 Answers4

4

I think your problem may be in your statement Their joint probability distribution should just be the two Boltzmann distributions in product. That may be true once the O2/N2 mixture that makes up the atmoshere and the CO2 volume have fully mixed, but until that occurs the unmixed gases have significantly different densities (as pointed out by @Thomas Fritsch), so the denser CO2 will displace the air and put out the candle.

Diffusive mixing of the two gas volumes will be a fairy slow process (diffusion coefficient of CO2 in air is 16 mm2/s) so the time for that to occur is long compared to the time for the gas displacement to take place.

The ideal gas laws do not take diffusion into account, so are not a suitable basis to use in analysing the problem.

Penguino
  • 3,466
4

As far as I know, CO$_2$ and O$_2$ both are almost perfect ideal gas at atmospheric conditions, so the volume they occupy shouldn't affect each other.

Room temperature CO$_2$ and O$_2$ can often be treated as ideal gases, but this is not one of those times. The issue is collisions. The mean free path of an air molecule (e.g. O$_2$) at STP is about 60 nm - an incredibly small distance. If you divided a container in half using a partition and filled one side with O$_2$ and the other side with CO$_2$, it would take an extremely long time (apparently on the order of 10 minutes) for the gases to mix completely once the partition was removed.

As a result, your CO$_2$ will tend to move as a fairly cohesive mass of fluid on the scale of seconds, which is the time scale you're studying when you dump it out onto a candle. This is also why we talk about air parcels and cold fronts in meteorology - distinct "packets" of air undergoing bulk motion tend to move around each other rather than mix together, because the time required for the latter is far longer than the time required for the former.

So really, the remarkable thing is not that ideal gas approximation fails, but rather that it so often succeeds. The key insight is that collisions cause a gas to relax toward equilibrium. Once that equilibrium is achieved, collisions no longer alter the macroscopic properties of the gas, and so as long as there are no appreciable long-range interactions between gas particles, the ideal gas approximation tends to yield the correct results. As soon as the gas is no longer in equilibrium - say, when the CO$_2$ is poured out of its container - the approximation fails badly until collisions have caused the system to equilibriate again.

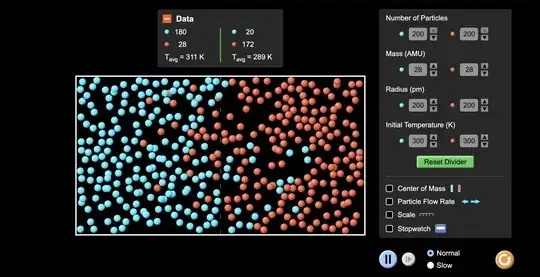
This excellent simulation from PhET illustrates precisely this phenomenon, so it's worth a look.

enter image description here

Albatross
  • 72,909
2

The important quantity is not pressure, but density. $CO_2$ is heavier than air. More exactly (from Carbon dioxide - Physical properties):

At standard temperature and pressure, the density of carbon dioxide is around $1.98\text{ kg/m}^3$, about $1.53$ times that of air.

That's why carbon dioxide sinks down in air, as long as the gases have not mixed yet.

Thomas Fritsch
  • 42,352
2

Analogous phenomenon: If I drop a sugar cube in a vat of water, it sinks to the bottom and sits for a while, even though the solubility of sugar in water is high—certainly enough for complete dissolution.

The key idea is that any cup of carbon dioxide in air has been specially prepared to be in a far-from-equilibrium condition, one that immediately starts evolving toward equilibrium.

Chemomechanics
  • 30,163