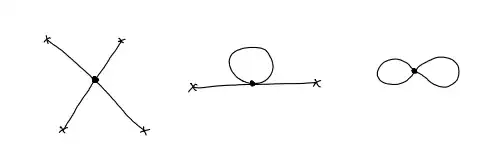
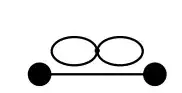
Starting from $S(\phi,J) = S_0(\phi) + S_{\rm int}(\phi) - J \phi$ with $S_0(\phi) = \alpha \phi^2/2$ and $S_{\rm int}(\phi) = \lambda \phi^4\!/4!$, the generating function(al) of the full model (including the interaction term) is given by $$ Z(J) = \frac{\int \! d \phi \, e^{-S_0(\phi)} e ^{-S_{\rm int}(\phi)} e^{J \phi}}{\int \! d\phi \, e^{-S_0(\phi)}e^{-S_{\rm int}(\phi)}} =: \left\langle e^{J \phi} \right\rangle,$$ which can be rewritten as $$Z(J) = \frac{\int \! d\phi \, e^{-S_0(\phi)} e^{- S_{\rm int}(\phi)} e^{J \phi}}{\int \! d\phi \, e^{-S_0(\phi)} } \cdot \frac{\int \! d\phi \, e^{-S_0(\phi)} }{\int \! d\phi \, e^{-S_0(\phi)}e^{-S_{\rm int}(\phi)} } = \frac{\left\langle e^{-S_{\rm int}(\phi)} e^{J\phi} \right\rangle_0 }{ \left\langle e^{-S_{\rm int}(\phi)} \right\rangle_0}, $$ where $\left\langle f(\phi) \right\rangle_0$ denotes the Gaussian mean value defined by $$\left\langle f(\phi) \right\rangle_0 := \frac{\int \! d\phi \, e^{-S_0(\phi)} f(\phi)}{\int \! d\phi \, e^{-S_0(\phi)}}. $$ The perturbative expansion of the term $\left\langle e^{-S_{\rm int}(\phi)} e^{J \phi}\right\rangle_0$ is given by $$ \left\langle e^{-S_{\rm int}(\phi)} e^{J\phi} \right\rangle_0 = e^{-S_{\rm int}(\partial_J)} \left\langle e^{J\phi}\right\rangle_0 = e^{-S_{\rm int}(\partial_J)} Z_0(J), $$ with the generating function of the free theory $Z_0(J)= \left\langle e^{J \phi} \right\rangle_0 = e^{J^2/2 \alpha}$, leading to the compact expression $$ Z(J) = \frac{e^{-S_{\rm int} (\partial_J)}Z_0(J)}{e^{-S_{\rm int}(\partial_J)}Z_0(J) \Large|_{J=0}}. $$ Expanding up to terms linear in $\lambda$, one finds $$e^{-S_{\rm int}(\partial_J)}Z_0(J) = e^{J^2/2\alpha} \left[1-\frac{\lambda}{4!}\left(\frac{J^4}{\alpha^4} +\frac{6 J^2}{\alpha^3}+\frac{3}{\alpha^2}\right) +\mathcal{O}(\lambda^2) \right].$$ With the help of the comments, you had realized yourself that you had simply forgotten the exponential term $e^{J^2/2 \alpha}$ in this expression. Note that the term in the denominator, $$e^{-S_{\rm int}(\partial_J)} Z_0(J) {\large|}_{J=0} = 1 -\frac{\lambda}{4!} \frac{3}{\alpha^2}+ \mathcal{O}(\lambda^2),$$ cancels all graphs with disconnected vacuum bubbles (like your last diagram), arriving at $$Z(J) = e^{J^2/2 \alpha} \left[ 1 - \frac{\lambda}{4!} \left( \frac{J^4}{\alpha^4} + \frac{6 J^2}{\alpha^3} \right)+ \mathcal{O}(\lambda^2) \right]$$ and $\left\langle \phi^2 \right\rangle =1/\alpha - \lambda/2 \alpha^3 +\mathcal{O}(\lambda^2)$.
Alternatively, employing the Wick theorem, you find $$\left\langle \phi^2 \right\rangle =\frac{\left\langle e^{-S_{\rm int}(\phi)} \phi^2 \right\rangle_0}{\left\langle e^{-S_{\rm int}(\phi)} \right\rangle_0 } = \frac{\left\langle \phi^2 \right\rangle_0 - \frac{\lambda}{4!} \left\langle \phi^6 \right\rangle_0+ \mathcal{O}(\lambda^2)}{1 - \frac{\lambda}{4!} \left\langle \phi^4\right\rangle_0 + \mathcal{O}(\lambda^2)} = \frac{\frac{1}{\alpha}- \frac{\lambda}{4!} \frac{15}{\alpha^3}+ \mathcal{O}(\lambda^2)}{1- \frac{\lambda}{4!} \frac{3}{\alpha^2}+ \mathcal{O}(\lambda^2)} = \frac{1}{\alpha} - \frac{\lambda}{2 \alpha^3} + \mathcal{O}(\lambda^2),$$ in agreement with the previous result.