Wavefunction of distinguishable spin 1/2 fermions

Question

Does the total wave function for distinguishable (i.e. not identical) spin 1/2 fermions need to be anti-symmetric under particle exchange? Or does the Pauli exclusion only hold for indistinguishable fermions?

Answer 1

Quoted from Pauli exclusion principle (emphasis by me):

A more rigorous statement is that, concerning the exchange of two identical particles, the total (many-particle) wave function is antisymmetric for fermions, and symmetric for bosons. This means that if the space and spin coordinates of two identical particles are interchanged, then the total wave function changes its sign for fermions and does not change for bosons.

Answer 2

No. Particles may be indentical but may or may not be indistinguishable. Indistinguishable particles will be described by a quantum state fully symmetric or fully antisymmetric under permutation.

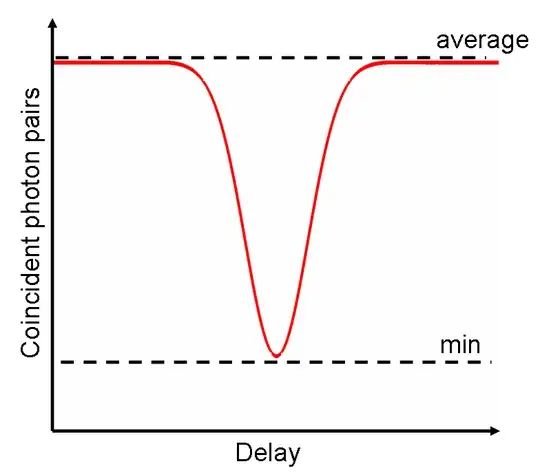
It is perfectly possible to have partially distinguishable particles: two photons with non-orthogonal polarization made to interact at a beam splitter are an example of system of partially distinguishable particles. If the photons are described by wave packets, then the overlap of the wave packets serves as a measure of distinguishability. The most spectacular example of this is the Hong-Ou-Mandel effect, where certain coincidence rates basically go to 0 only when the photons are fully indistinguishable:

In the figure, the overlap between two Gaussian wave packets is tuned using an ajustable delay. When the two packets overlaps and the photons are fully indistinguishable, there is no probability of the two photons exiting to different ports of the interferometer. As one increases the distinguishability, this probability increases.

If you’re looking for an example with two fermions, imagine two wave packets describing identical spin-1/2 fermions but such that the wave packets are only partially overlapping. In this case the state is described by a linear combination of a fully symmetric state, and a fully antisymmetric state (here we’re talking about symmetric/antisymmetric w/r to the action of the permutation group $S_2$), and the coefficients are such that, as the wave packets fully overlap, only the antisymmetric combination remains. Indeed the HOM experiment has been done with electrons, as reported in

Liu, R. C., et al. "Quantum interference in electron collision." Nature 391.6664 (1998): 263-265

and in

Oliver, William D., et al. "Hanbury Brown and Twiss-type experiment with electrons." Science 284.5412 (1999): 299-301.

Note the similarity between the results of Oliver:

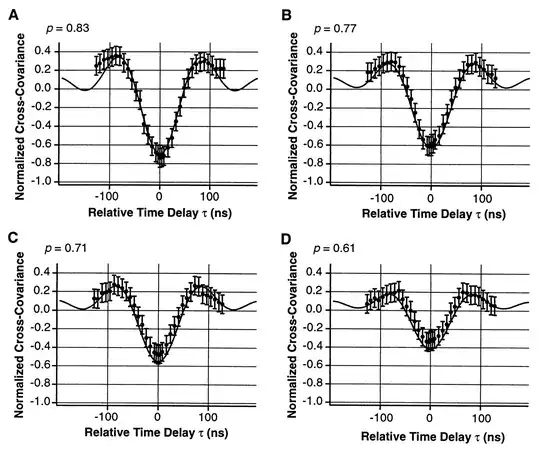
and the results of Hong et al.