Seeking expression for radial velocity of an object in an elliptical orbit (with focus at coordinate origin) as function of radius

Question

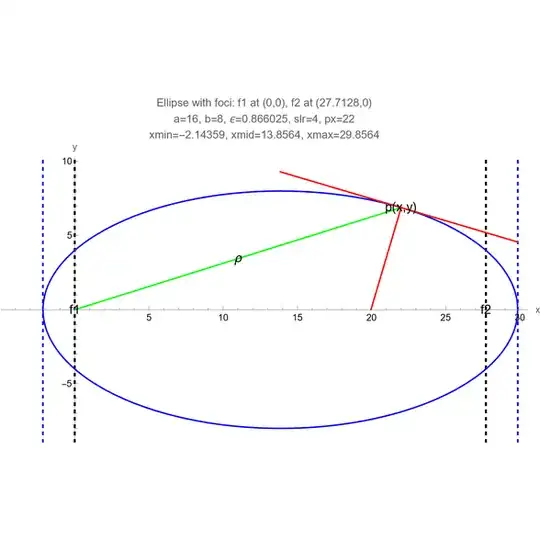
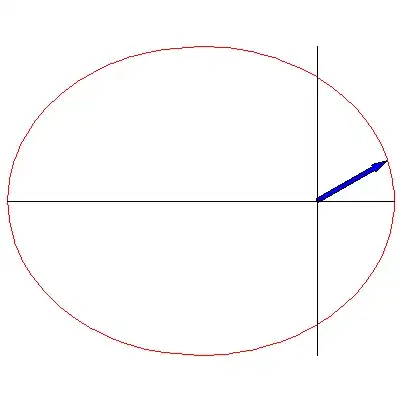
Consider a planar, elliptical orbit in a simplified two body, $\frac{K}{r^2}$ central attractive force problem (i.e. assume $m1 >> m2$ so focus $f1$ is effectively at $m1$, with $m2$ at point $p\left(x,y\right)$) and $\rho$ being the radius (green line) from $m1$ to $m2$ ($f1$ to $p\left(x,y\right)$), as indicated in the following plot ($f1$ at coordinate origin, periapsis at left blue hash, apoapsis at right blue hash):

I am trying to determine the expression for (what I am referring to as) the radial velocity $v_\rho=\frac{d\rho}{dt}$ along the direction of $\rho$ toward $f1$, at each point $p\left(x,y\right)$ on the orbital ellipse, strictly as a function of $\rho$. To be clear, I do not seek the expression for the velocity tangent to or normal to (red lines in plot) the orbital ellipse at point $p\left(x,y\right)$, but rather only the velocity along $\rho$ toward $f1$.

I have tried to come up with this expression using the very illuminating discussion in this item How do we describe the radial velocity in elliptical orbits?, but with no success yet. I also thought this might be readily found in a classical mechanics text (e.g. Symon), but haven't found (or recognized) such.

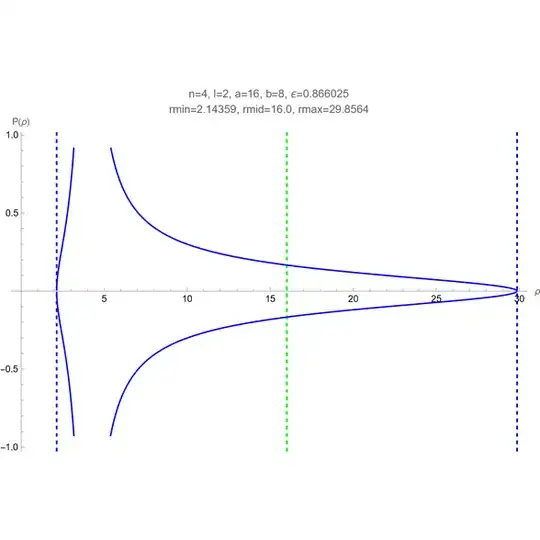
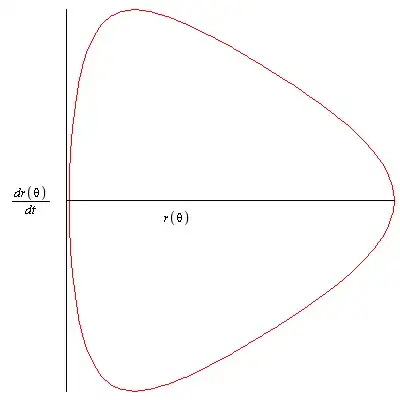
In line with How do we describe the radial velocity in elliptical orbits?, I expect the plot of this radial velocity to be structurally similar to the following but with a continuous, finite value - unlike the infinity exhibited in this plot - for the latus rectum at $\rho=4$ (note that $\dot{\rho}=0$ for periapsis at $\rho\approx+2.14359$ in the plot below, which differs from periapsis at $x\approx-2.14359$ in the elliptical orbit plot above):

Any reference to an existing solution, or advice on deriving one, would be greatly appreciated.

I think I have provided enough information to fully characterize the problem, but can certainly provide more info if I've missed something.

Answer 1

In this answer, I use the convention where the ellipse has the periapsis on the right, which is the opposite to your diagram.

The polar equation of the ellipse aligned with the axes, with the origin at the focus and the major axis on the X axis, with semi-major axis $a$ and eccentricity $e$ is

$$r = \frac{p}{1 + e\cos\theta}$$

where $p = a(1-e^2)$ is the semi-latus rectum. The periapsis is at $\theta=0$, the apoapsis is at $\theta=\pi=180°$.

The specific angular momentum is the angular momentum per unit mass. Angular momentum is conserved in an isolated system, so $h$, the magnitude of the specific angular momentum vector, is constant. It can be shown that $$h^2 = \mu p$$ and $$h = r^2\omega$$ where $$\mu = G(m_1 + m_2)$$ is the gravitational parameter and $$\omega = \dot\theta = \frac{d\theta}{dt}$$ is the angular velocity.

Differentiating the equation for $r$ with respect to time, we get

$$\begin{align} \dot r & = p(1+e\cos\theta)^{-2}(e\sin\theta)\omega\\ & = \frac{r^2\omega}{p} \left(e\sin\theta\right)\\ \dot r & = \frac{h}{p} \left(e\sin\theta\right)\\ \end{align}$$

We can now create a parametric plot of $r$ and $\dot r$ using $\theta$ as the parameter. But we can express $\dot r$ in terms of $r$ via the Pythagorean identity, $$cos^2\theta + \sin^2\theta = 1$$ After some algebra, we get $$\dot r^2 = \mu\left(\frac2r - \frac{p}{r^2}-\frac1a\right)$$ Note that the vis-viva equation is $$v^2 = \mu\left(\frac2r - \frac1a\right)$$ where $v$ is the (tangential) speed.

Thus $$\dot r^2 = v^2-\mu\left(\frac{\mu p}{r^2}\right)\\ = v^2-\left(\frac{h}{r}\right)^2$$

Incidentally, $$v^2 = \frac{\mu}{p}\left(1+2e\cos\theta+e^2\right)$$

---

Here's a parametric plot for $a=5, e=3/5$, using "natural" units, so that an orbit with $a=1$ has an orbital period of $1$. In our Solar System, that corresponds to solar orbits measured in AU (astronomical units) and years. In such units, where the orbiting body has negligible mass, $\mu = 4\pi^2$.

Here's the corresponding orbit plot.

The coloured dots correspond to equal 15° steps of $\theta$, starting at red and going around the hue cycle, through orange, yellow, green, cyan, blue, magenta, and back to red.

Here's the plotting script, in Sage / Python. The script can also plot $\dot r$ as a function of $r$, but that's currently commented out.

Here's the orbit plotting script. And here's a "combo" script that can do both graphs, on the same plot, if desired.

Answer 2

The polar equation of the ellipse

$$\mathbf r=r(\theta)\begin{bmatrix} \cos(\theta) \\ \sin(\theta) \\ \end{bmatrix}\quad, r(\theta)={\frac {p}{1+e\cos \left( \theta \right) }}$$

thus $~\dot{\mathbf{r}}\cdot\mathbf e_r~$ equal to

$$\dot r(\theta)=\frac{\partial r}{\partial \theta}\,\dot\theta=\frac{\partial r}{\partial \theta}\,\frac{h}{r^2}={\frac {e\sin \left( \theta \right) h}{p}}$$

with: $$p=a\,(1-e^2)\quad,h=\sqrt{\mu\,p}\quad,\mu=G\,(m_1+m_2)\quad\Rightarrow\\ \dot r={\frac {e\sin \left( \theta \right) \sqrt {\mu\,a \left( 1-{e}^{2} \right) }}{a \left( 1-{e}^{2} \right) }} $$

Answer 3

I posted the question that you referenced and now do have a couple ways to find the radial velocity of an elliptical orbiting body.

If you know the radial velocity (k in the figures below) at the latus rectum, k can be found at any other point if you know the angle value of the true anomaly. See Fig 1 equations 3 and 8.

An alternate method to find radial velocity k is done by calculating the acceleration along r planet-to-body over time as in Fig 2. Fig 1 equation 11 provides the instantaneous net acceleration of the orbiting body. Using that over time (.76 seconds here) and an approximate change in radial velocity k is calculated.

Where the net acceleration comes from:

A body in motion always has a radial velocity with respect to a point in the direction toward or away from that point and the magnitude of the radial velocity is always changing, or more importantly, always in a state of change. The exception is when the body’s velocity is aligned with the point where there is no radial velocity but when the body’s velocity is perpendicular to the point, as in circular motion, the magnitude of the radial velocity is zero yet is also in a state of change as explained below.

Fig 3 shows a body in motion doing a fly-by of point C. The equation for rd provides the distance of rd over time. The first derivative of rd provides the magnitude of the radial velocity k. The second derivative of rd provides the instantaneous change in radial velocity k. p^2/rd does the same thing.

Fig 4 - The second derivative of rd also has an interesting simplification to the centripetal acceleration formula when the fly-by body is in the position of a rotating body (perpendicular velocity to the center point of rotation).

The orbiting body has a radial velocity that is always in a state of change in the direction away from the planet. In other words, the body is always in a state of acceleration away from the planet. So, there is a net acceleration found in the difference of gravity and this radial state of change.

This is stuff I came up with and haven't yet found this approach using a net acceleration so I may be wrong but the numbers work. The same goes for the centripetal acceleration derivation.