How do we describe the radial velocity in elliptical orbits?

Question

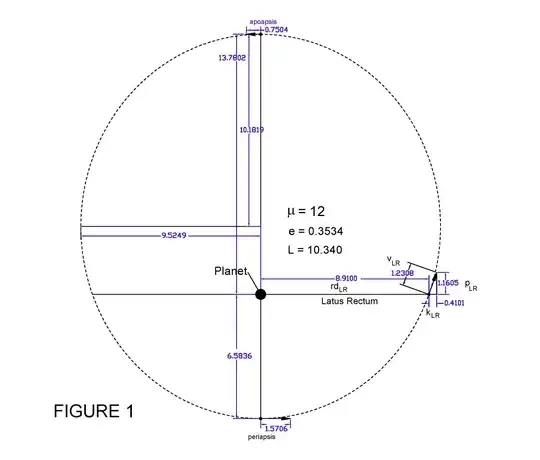
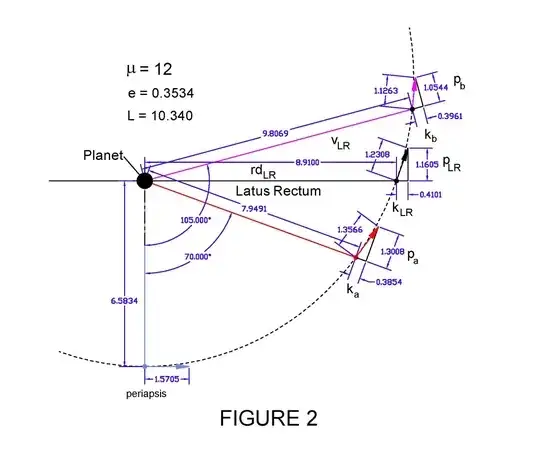
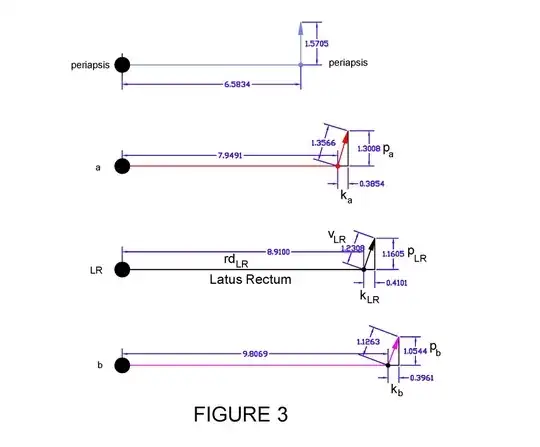
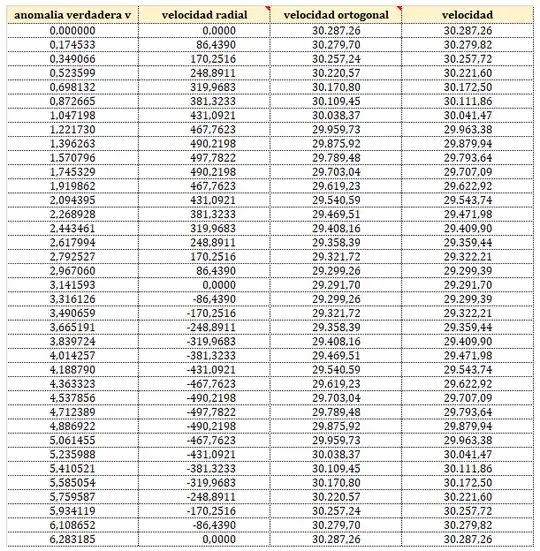
When I look at the velocities of elliptical orbiting satellites the radial velocity (k in the figures) increases from zero magnitude at periapsis, to a maximum at the latus rectum, then back down to zero at the apoapsis. This describes a rate of increase opposite the direction of gravity that changes over time.

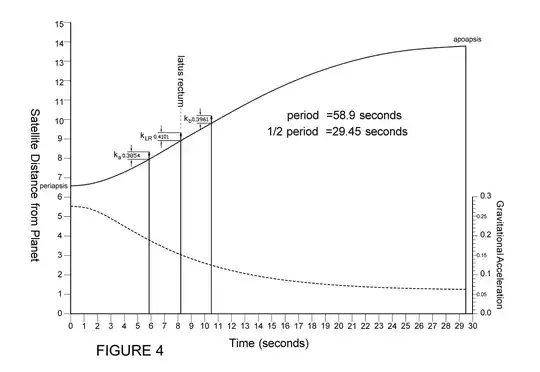
From periapsis to the latus rectum, the satellite to planet distance increases at an increasing rate. Then from the point of the latus rectum to the furthest point, apoapsis, this distance increases at a decreasing rate.

The change in distance describes a net acceleration away from the planet until the satellite reaches the latus rectum where the net acceleration reverses direction - in the same direction as gravity. This occurs despite the fact that gravity is in one direction and is decreasing in magnitude throughout the periapsis to apoapsis satellite journey.

What is the math that we use to calculate the radial velocity?

When the satellite crosses the latus rectum, the radial velocity k decreases. Fig 4 reveals that the rate of change in distance from the planet decreases at that point which agrees with the change of radial velocity k. There is a point of inflection at the latus rectum which means there would be a mathematical change of sign. Is there math out there that describes this change of sign?

What is the physics we use to describe why the radial velocity does what it does? I’m not looking for a geometrical answer here. We should be able to describe this physically like we do with any other thing in motion experiencing a force and acceleration. I just can’t find any mention of it in my searches.

Answer 1

You are making a common mistake in assuming that the radial acceleration is the time rate of change of the radial velocity. In Cartesian coordinates we can apply this reasoning because the unit vectors are constant. However, in polar coordinates the unit vectors depend on the spatial coordinate.

For planar motion using polar coordinates, the radial acceleration actually has two terms: $$a_r=\ddot r-r\dot\theta^2$$

where $\ddot r$ is the time rate of change of $\dot r$, which is the time rate of change of the radial coordinate $r$, and $\dot\theta$ is the time rate of change of the polar coordinate $\theta$.

As you can see, $\ddot r$ is not the whole picture. Even if $\ddot r>0$ this does not mean that $r\dot\theta^2<\ddot r$. In fact, if $\ddot r$ is positive then $r\dot\theta$ has to be larger than $\ddot r$, because the net acceleration has to always point in the negative $\hat r$ direction if the only force acting on the satellite is gravity which points inwards towards the planet.

To help you further, since we know that $a_r=-GM/r^2$, we can express the rate of change of $\dot r$ as $$\ddot r=r\dot\theta^2-\frac{GM}{r^2}$$ This should show you how the radial velocity can oscillate, as these two terms will change in magnitude throughout the orbit, thus changing the sign of $\ddot r$.

When examining the gravitational acceleration along a line from planet to satellite we see an increase in distance that describes an acceleration away from the planet - proven by the radial velocity change - until the satellite reaches the latus rectum. If you had a rocket, with its thrust, accelerating directly away from the planet until it reaches a certain distance where it reverses the thrust direction it could mimic exactly what we see along that planet to satellite line described here.

These aren't the same scenario. Just because we can choose to focus just on $r$ does not mean it is the only relevant coordinate. The satellite is still orbiting around the planet; the satellite is not moving along a 1D path described by $r(t)$ like you are proposing with your rocket. We are dealing with polar coordinates and vectors, and care needs to be taken before you simplify the analysis by considering scalar, Cartesian values instead.

Answer 2

What is the math that we use to calculate the radial velocity?

With the usual nomenclature:

$G$ = universal gravitational constant

$M$ = mass of primary

$m$ = mass of secondary

$a$ = semi-major axis of the elliptical orbit

$e$ = eccentricity of the elliptical orbit

$\theta$ = true anomaly

$r$ = radius vector (position vector from de focus)

The mathematical expression to calculate the radial velocity is:

$$v_r=\sqrt{\frac{G (M+m)}{a(1-e^2)}} \ \ e \sin \theta$$

And the expression for the velocity component perpendicular to the radius vector is:

$$v_{\theta}=\sqrt{\frac{G (M+m)}{a(1-e^2)}} \ \ (1+e \cos \theta)$$

Naturally, it follows that:

$$v=\sqrt{v_r^2+v_{\theta}^2}$$

That operating can be converted into the familiar expression:

$$v=\sqrt{2 G (M+m)\left ( \frac 1 r - \frac 1{2a} \right )}$$

$$v=\sqrt{2 \mu \left ( \frac 1 r - \frac 1{2a} \right )}$$

Where $\mu=G(M+m)$ is the gravitational parameter.

The mathematics required to detect the maxima and minima of a function consists of calculating the places where the derivative of the function is zero.

The derivative of the radial velocity with respect to the true anomaly is:

$$\frac{dv_r}{d\theta}=\sqrt{\frac{G (M+m)}{a(1-e^2)}} \ \ e \cos \theta=0 \rightarrow \cos \theta =0$$

$$\displaystyle \theta=\frac{\pi}2 \qquad or \qquad \theta=\frac{3\pi}2$$

Which corresponds to the two "semilatus rectus".

$\theta=0 \longrightarrow v_r=0$

$0<\theta <\dfrac{\pi}2 \longrightarrow v_r>0$ increasing positive value

$\theta=\dfrac{\pi}2$ maximum positive value of $v_r$

$\dfrac{\pi}2 <\theta < \pi \longrightarrow v_r>0$ decreasing positive value

$\theta=\pi \longrightarrow v_r=0$

$\pi<\theta <\dfrac{3\pi}2 \longrightarrow v_r<0$ increasing module of negative value

$\theta=\dfrac{3\pi}2$ maximum module of the negative value of $v_r$

$\dfrac{3\pi}2<\theta < 2\pi \longrightarrow v_r<0$ decreasing module of negative value

$\theta=2\pi \longrightarrow v_r=0$ And we have made a complete turn

I attach, as an example, a table with the radial velocity, the perpendicular velocity and the total velocity (metres per second) of the Earth in its elliptical orbit around the Sun, as a function of the true anomaly (radians)

Best regards