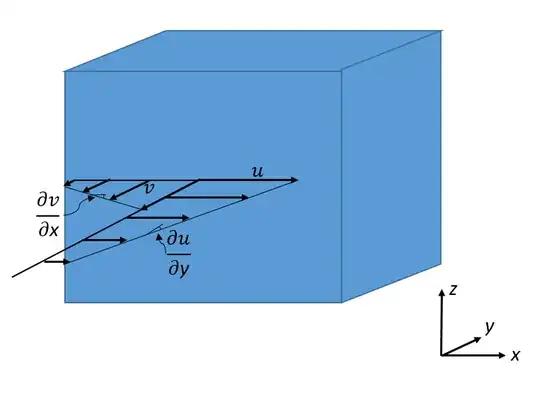
I drew a image below. For that face, of normal $y$, we have that the shear stress acting on the $x$ direction is:
$$ \tau_{yx} = \mu(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x})$$
with $\mu$ the viscosity, $u$ the along-$x$ velocity, and $v$ the along-$y$ velocity. Now, I understand that a gradient in $u$ velocity in $y$ creates a $ \tau_{xy} $, i.e a shear in $y$. But I do not understand how is that shear a function of $\frac{\partial v}{\partial x}$, which in my mind should only give a shear on faces of normal $x$. I do know that for rotational equilibrium shear stresses are symmetric, so that $ \tau_{xy} = \tau_{yx} $. But this to me does not explain conceptually why $\frac{\partial v}{\partial x}$ is giving a shear on a surface of normal $y$. Can you please provide an explanation? Similar question can be made for each of the other faces, of course.