Can Stern-Gerlach spin alignment be seen as a result of EM radiation of precessing magnetic dipole?

Question

Stern-Gerlach experiment is often seen as idealization of measurement. Using strong magnetic field, it makes magnetic dipoles (of e.g. atoms) align in parallel or anti-parallel way. Additionally, gradient of magnetic field bends trajectories depending on this choice.

Magnetic dipoles in magnetic field undergo e.g. Larmor precession due to $\tau=\mu \times B$ torque, unless $\mu \times B =0$ what means parallel or anti-parallel alignment.

Precession means magnetic dipole becomes kind of antenna, should radiate this additional kinetic energy. Thanks to duality between electric and magnetic field, we can use formula for precessing electric dipole, e.g. from this article:

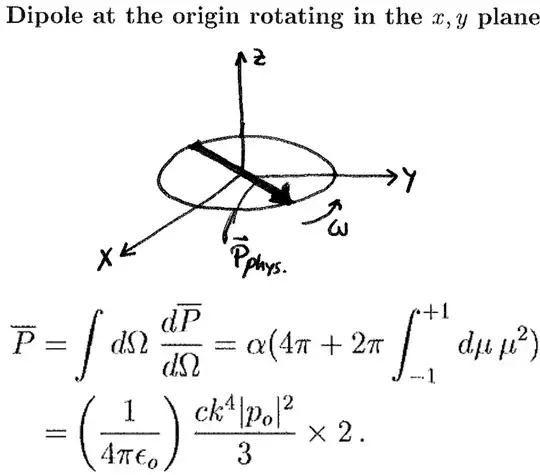
Using which I get power like $10^{-3} W$, suggesting radiation of atomic scale energies ($\sim 10^{-18}J$) in e.g. femtoseconds (to $\mu \times B=0$ parallel or anti-parallel).

So can we see spin alignment in Stern-Gerlach as a result of EM radiation of precessing magnetic dipole?

Beside photons, can we interpret other spin measurement experiments this way?

---

Update: Connor Behan below has found very nice article "Phenomenological theory of the Stern-Gerlach experimen" by Sergey A. Rashkovskiy with detailed calculations - getting $\sim 10^{-10}$s times for such alignment of atoms in Stern-Gerlach: https://www.preprints.org/manuscript/202210.0478/v1

Instead of energy radiation (are they equivalent?), it directly uses below formula ((3) in article) for dynamics of magnetic dipole $v$ of gyromagnetic ratio $\gamma_e=-e/m_e c$ in external magnetic field $H$, $b$ is semi-classical calculated parameter : $$ \dot v = \gamma_e\, v \times H - 2\alpha\, v \times \dot{v} +\frac{b}{c}\, v\times \ddot{v} $$

Update: Analysis of EM waves radiated by rotating dipole: http://web.hep.uiuc.edu/home/serrede/P436/Lecture_Notes/P436_Lect_13p75.pdf

Answer 1

As always, it depends how far you want to push the analogy. The general answer to whether you can model quantum effects with classical mechanics is no. For example, electrons would have to rotate faster than the speed of light to have their spin angular momentum interpreted as a type of orbital angular momentum.

In the case of the Stern-Gerlach experiment, the limitations of a classical approach were discussed quite well in a previous question. Larmor precession is reproduced in the sense of Ehrenfest's theorem. When there's a constant magnetic field $\textbf{B}$ perpendicular to the direction of initial spin, the time dependent state for a spin-half atom looks like \begin{equation} \sqrt{2} \left | \psi(t) \right > = \exp(i\mu_B B t / \hbar) \left | \uparrow \right > + \exp(-i\mu_B B t / \hbar) \left | \downarrow \right >. \quad (1) \end{equation} This means you can take the expectation of the spin operator and find $\left < S_x(t) \right > = \frac{\hbar}{2} \cos(\mu_B B t / \hbar)$. But unlike with macroscopic particles, this is a statistical statement. Each measurement will only give $\left | \uparrow \right >$ or $\left | \downarrow \right >$ because we were not starting off with a system having many Bohr magnetons worth of magnetic moment. It had the "minimal" magnetic moment leading to just two terms in (1). Note that you could account for energy radiating away as you say to give $S_x$ more non-trivial time dependence but this will not change the quantization of $S_z$.

This quantization should be built into the formalism we use. Indeed, the Stern-Gerlach apparatus is good not just for aligning dipoles along a certain axis but separating the positive and negative ones due to inhomogeneities in the field. So silver atoms (even a large number of them) end up hitting two points on the detector whereas larger particles in the classical regime hit a continuum corresponding to the fraction of their magnetic moment which lies in the direction of $\textbf{B}$.

But the most interesting finding related to Stern-Gerlach is what happens when you use it many times in succession with different axes. If you run $SG_z$ keeping the $+z$ eigenvalue and follow it by $SG_x$ keeping $+x$, a quantum mechanical treatment correctly predicts that the intensity of the beam decreases by half each time. Classically, if you imagine that the beam after $SG_z$ is in the $+z$ direction because you have waited for other components to decay away, its projection onto $+x$ obtained by $SG_x$ would just be zero. Finally, a classical magnetic moment at a $45^\circ$ angle (involving $+x$ and $+z$) will never have a projection in the $-z$ direction. However, in the above experiment, $SG_x$ destroys the information about how $SG_z$ filtered the beam initially therefore allowing equal numbers of $\left | \uparrow \right >$ and $\left | \downarrow \right >$ detections when you run $SG_z$ once again. This is a demonstration of the uncertainty principle for spin operators.