Why is gravity not a force?

Question

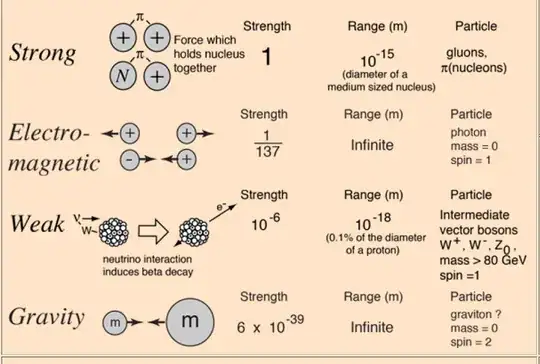
Gravitation is the mutual attraction of masses, yet Einstein showed it is how spacetime is curved by mass and how mass moves in relation to this curvature. Why then do we still consider gravitation a "force"?

Answer 1

The need for the concept of "fundamental force" comes from quantum mechanics, where a fundamental force is assigned a coupling constant that enters the quantum mechanically modeled interactions. Mainstream physics assumes a form of general relativity that is quantized, and quantization needs a coupling constant for the interaction with the space time of GR.

At present GR is not definitively quantized; an effective quantization of gravity(GR) is used in most cosmological model efforts. That is why the term "fundamental force" is used for gravity.

These are the coupling constants for all the mainstream "forces" that are used in quantum mechanical theoretical models.

Answer 2

[gravity] is not really a force at all

This is true and it isn't, but beside the point anyway as we're best talking about fundamental interactions, not forces, so as to include decays. The weak interaction, for example, does exert forces, but they're so feeble it primarily matters because of the decays it causes.

Isn't the "true" fundamental interaction that between mass and spacetime?

@annav's answer already noted fundamental interactions are of quantum-mechanical significance. There are any number of reasons gravity must be quantum. Therefore, GR must emerge from the effects of gravitons. The most fundamental account of gravity is therefore in terms of how particle interactions affect the spacetime in which particle interactions are suited. (However, there's a bit more to being a fundamental interaction than having a particle-based - or to be more precise, field-based - explanation.)

Is this because some physicists don't really believe in GR?

Having said all that, even if the universe weren't quantum in the slightest, it still would make sense to consider gravity a fundamental interaction. Such a universe would have "classical" field theories for electromagnetism and gravity, and the latter would be GR or an alternative. It would be a gauge theory like EM, except based on diffeomorphism invariance rather than local $U(1)$. Field theories' Lagrangians' kinetic terms would use an alternative to partial derivatives that adds two kinds of term, those proportional to the EM field for EM, plus those proportional to Christoffel symbols for GR. See also here & here for further parallels.