Given the 4D Yukawa Lagrangian
$$\mathcal{L} = \frac{1}{2} (\partial_\mu \phi)(\partial^\mu \phi) - \frac{1}{2} m^2 \phi^2 + \bar\psi(i\not\partial-m)\psi+ g \bar{\psi} \phi \psi \tag{1}$$
The theory with counterterms is given as
$$\mathcal{L}^c = \frac{1}{2} (\partial_\mu \phi)(\partial^\mu \phi)(1+\delta_z) - \frac{1}{2} \phi^2 (m^2+\delta_m) + \bar\psi(i\not\partial(1+\delta_z')-(m+\delta_m'))\psi- (g+\delta_g) \bar{\psi} \phi \psi \tag{2}$$
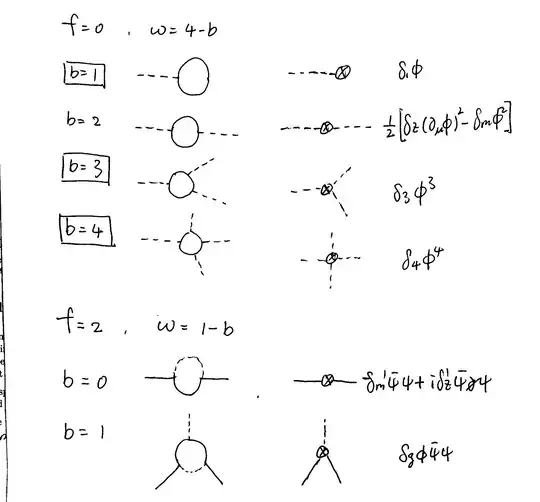
For the term $g\phi\bar\psi\psi$, we can find the superficial degree of divergence as $$\omega = 4-(3/2)f-b, \tag{3}$$ where $f$ and $b$ are the numbers of external fermion and scalar legs of Feynman diagrams. Then, I can draw all the possible divergent diagrams as follows:
My question is about the three boxed cases: I don't think I can find the associated terms in $\mathcal{L}^c $. Why they are not included? In this case ($\phi^3$ theory), we included $-\delta_1\phi$ in the Lagrangian, so I wonder if we should do something similar in this case.