0

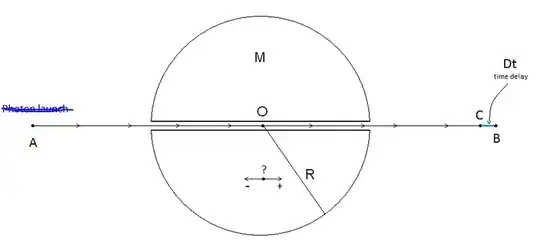
The diagram below I have borrowed from another question about Shapiro Time Delay: Impossible dilemma about Shapiro delay and momentum conservation

enter image description here

My question is if Shapiro time delay applies to massive objects. So in the diagram above, imagine A is some mass traveling the path through the mass M. In the case of a photon, Shapiro time delay means the photon will appear to slow its rate of travel as a result of M, at least to a non-local observer. I know the effects of curved spacetime would mean A would accelerate as it moves toward M, and then decelerate as it starts to try to move away from it, again as observed by a non-local observer. But is there also a component of its movement which lowers the velocity due to M?

HardlyCurious
  • 319

1 Answers1

1

Yes it does.

The Shapiro delay happens because as seen by distant observer light travels more slowly than $c$ near a massive object (it's actually more complicated than this, but we'll go with this interpretation for now). The slower speed means it takes longer to cross the region of space near the massive object than expected.

So the question is does this happen for massive objects as well, and the answer is that it does. Suppose we consider a small object falling from infinity towards some large mass $M$. In Newtonian gravity we just equate the kinetic and potential energy:

$$ \tfrac12 mv^2 = \frac{GMm}{r} $$

To get the velocity as a function of $r$:

$$ v_{\text{Newt}}(r) = \sqrt{\frac{2GM}{r}} $$

But if we include relativistic effects this equation is modified to:

$$ v_{\text{GR}}(r) = \left(1 - \frac{2GM}{c^2r}\right)\sqrt{\frac{2GM}{r}} $$

So:

$$ v_{\text{GR}}(r) = \left(1 - \frac{2GM}{c^2r}\right)v_{\text{Newt}} $$

The quantity in the brackets, $\left(1 - 2GM/c^2r\right)$ is less than one so the velocity when we take general relativity into account is less than the velocity Newton would have calculated. So massive objects also show their own version of Shapiro delay.

John Rennie
  • 367,598