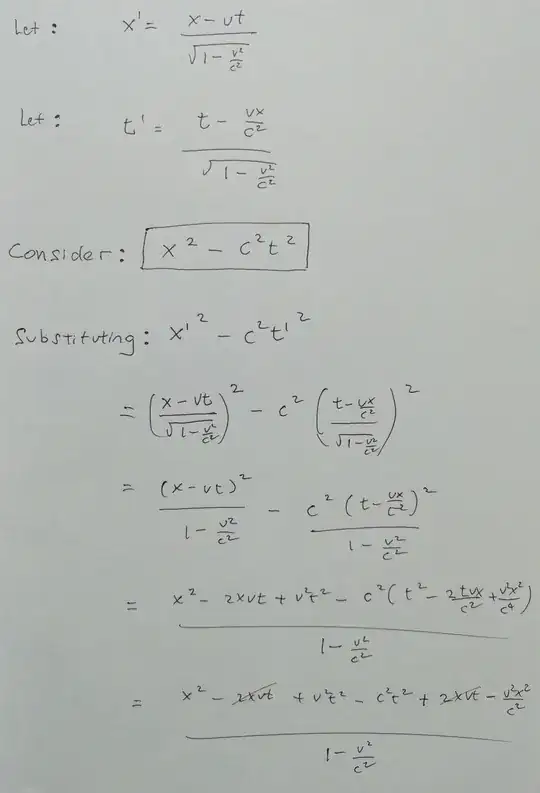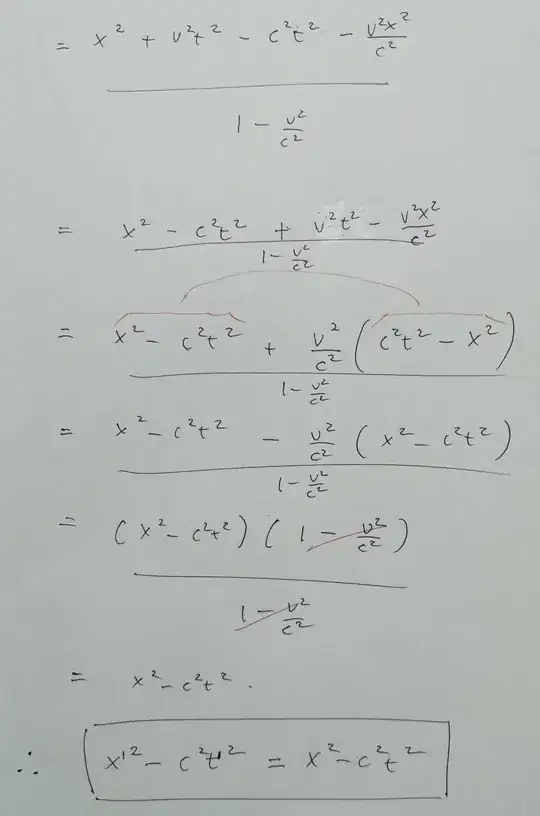The algebraic criteria for proving Lorentz invariance is that, replacing x with x' and t with t', where
$$x'=\gamma(x-vt)$$ $$t'=\gamma\left(t - \frac{vx}{c^2}\right)$$
should give back a certain "similar" form of the original equation.
What is the simplest toy equation that can be easily shown to be Lorentz invariant algebraically?
$\Delta t^2-\Delta (x/c)^2=\Delta s^2$ for Minkowski spacetime geometry,
in analogy to $\Delta x^2+\Delta y^2=\Delta r^2$ for Euclidean geometry
Is there a formal definition of simplest? I'll posit:
$$ E^2 -(pc)^2 = (mc^2)^2 $$
which you can Lorentz transform to $|\vec p| = 0$ and get:
$$ E = mc^2 $$
Of course there is the notion of "Manifest covariance" (which is manifest invariance for Lorentz scalars like $m$), in which covariance is apparent in Minkowski space:
$$ p^{\mu}p_{\mu} = (mc)^2 $$
where the 4-momentum is:
$$ p^{\mu} = (E/c, \vec p) $$
Finding invariant equations in special relativity is relatively easy once you know about contra/covariance.
Define a contravariant vector as any vector which transforms as $$V'=\Lambda\cdot V^\nu$$ where $${\Lambda}=\pmatrix{\gamma&-\beta\,\gamma\\ -\beta\,\gamma&\gamma}$$ Is the Lorentz matrix. Contravariant vectors are often denoted with a superscript index, like $V^\mu$. Now define a covariant vector as a vector which transforms as $V'=({\Lambda^{-1})^T}\cdot V$, here $\Lambda^{-1}$ is just the inverse of the Lorentz matrix and you can find it by replacing $\beta\rightarrow-\beta$. Here $^T$ means taking the transpose. Contravariant vectors are often indicated with a subscript index, like $V_\mu$.
Now every time you contract a contravariant vector with a covariant vector you get an expression which is invariant under Lorentz transformations. A contraction is then defined using either of these expressions $V\cdot W=V_\mu W^\mu=V^TW$. \begin{align} V'\cdot W'&=V'_\mu W'^\mu\\ &=((\Lambda^{-1})^TV)^T \Lambda W\\ &=V^T\Lambda^{-1}\Lambda W\\ &=V^TW\\ &=V\cdot W \end{align} If you have a contravariant vector you can easily construct a covariant vector by contracting it with ${\eta_{\mu\nu}}=\pmatrix{-1&0\\0&1}$. For example if you contravariant vector is $(ct, x)$, your covariant vector is $(-ct, x)$. Contracting these gives $-c^2t^2+x^2$, which is invariant.
The quantity
$$x^2 - c^2t^2$$
is algebraically invariant under the transformation:
$$x'=\gamma(x-vt)$$ $$t'=\gamma\left(t - \frac{vx}{c^2}\right)$$
