What is the true quantum description of electron transport in solids?

Question

Im currently struggling to understand the quantum description of electrical current in a solid. Applying the linear combination of atomic orbitals and applying the Bloch theorem we can get different electron energies for different crystal wave vectors as described by the E(K) diagram. However the electrons wave function is spread evenly across the lattice. This makes the quantum model of current problematic. Changing the wave vector only changes the phase of the adjacent atomic orbitals in the lattice and correspondingly the electron energy. It does not describe how the electron moves in a solid. More specifically this model (to my understanding) does not explain how charge can build up on a capacitor plate when we apply a voltage, as this would need to have regions of higher electron density.

My understanding of how the electron wave should move is as follows:

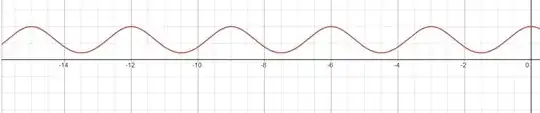
Above images shows a 1D chain of hydrogen atoms with the corresponding 1S orbital wave functions plotted. The equations describing the orbital wave functions are in a simplistic form, ie not exact as I only care about how the curve looks. First I know that adjacent wave functions should overlap to form one continuous molecular orbital, de-localised over the entire crystal:

Here I have assumed K=0 (ie the fully bonding state)

Edit: The new summed wave function can only hold tow electrons only. It is the very bottom bonding state of the energy band.

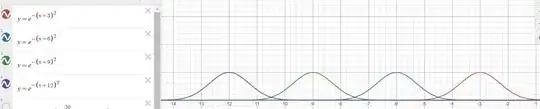
Now if I allowed this to be a simple travelling wave then applying an electric field would not allow for any charge to build up on one side of a conductor (for example, if I brought a metal sphere close to a van-de graaff generator) . However If I localise it by tacking on another Gaussian term I get a localised wavefunction:

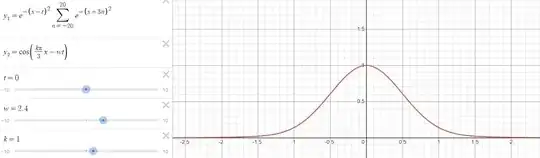
Now If I apply an electric field (to my understanding) tow things will vary, the phase of the 1S orbitals given by the travelling crystal wave vector and the amplitude given by the wave packet:

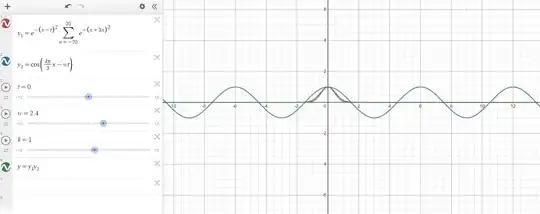
Here the green curve is the total electron wave function at t=0, the blue curve is the crystal wave (from Bloches theorem) and the red curve is the original wave packet. I now vary time from 0 to 4 seconds:

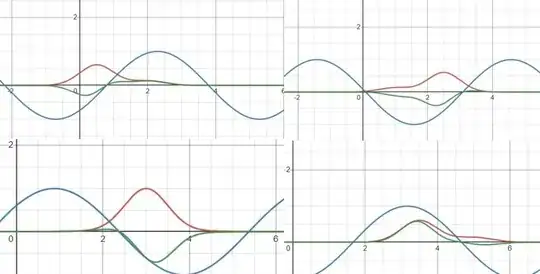
Top left image is showing the wave function at t=1 whilst the bottom right is at t=4. Images ordered from left to right.

Is this what the electron wave looks like as it propagates through the crystal? To me it makes some degree of sense as it would allow electrons to accumulate in certain regions under an applied electric field like a capacitor plate and would also allow for scattering of electrons through defects.

Is my understanding correct?

Update:

Just had an extra thought on electron localisation. In a filled band the electrons are forced to take on certain energy states. They cannot change K values as they are filled which means the uncertainty in our K is zero. This means our uncertainty in the position is infinity large, ie the electron is de-localised over the entire crystal given by Heisenberg's certainty principle:

$$\Delta \chi \Delta \rho \geq \hbar / 2 \, . $$

Therefore there is no electron localisation (where x is position). However if we looked at an empty or partially filled band, there is a certain degree of probability than an electron can occupy a certain K value. The electrons can fill these states with a certain probability given by the Fermi Dirac distribution: $$f(E) = \frac{1}{e^{(E - E_f)/kT} + 1} \, .$$

Clearly the uncertainty in the K value will now be none zero which decreases our uncertainty in the position. Now our electron can become a localised wave packet, made up of may probable K positions:

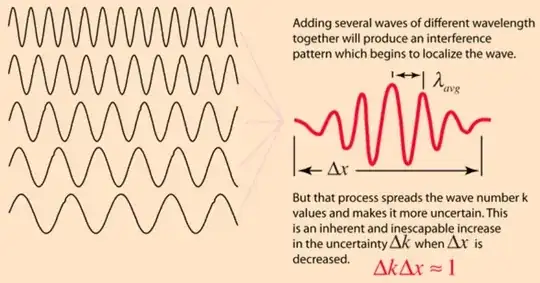
For a change in temperature, or an absorption of a photon, the K distribution will be skewed towards higher or lower K values, giving a faster or slower travelling wave packets. This now makes total sense (if correct). Valance bands cannot conduct as there is no preferred direction of travel. ie under an electric field the wave function can barely distort and is related entirely on atomic Polarizability as the uncertainty in X is near infinite. Therefore no conduction takes place. In an unfilled band the uncertainty in the K values is now none zero giving wave packets. If I applied an electric field to a capacitor plate, those wave packets can move to the surface of the plate, creating a bias in electron density at the surface giving a net charge.

I think I understand this now, but there is one final problem, and thats with the mathematical description of wave packets. They are still periodic functions:

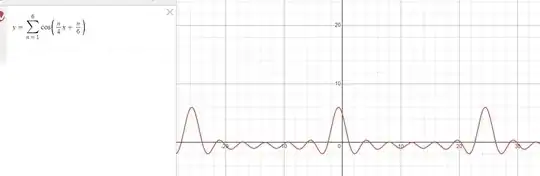
As shown above for a random wave packet model, there will be certain periodic positions where all the component of the wave becomes in phase. This is a little troublesome for me as this will mean an electron whilst localised still has a periodic wave packet. I would have thought there would be a single wave packet for an electron.

I feel im close to fully understanding the quantum description, but i still cannot seem to answer how there is periodic wave packets rather than only 1.

Answer 1

I think that the image you have sketched is merely a classical "toss electron balls around" married with a little bit of Gaussian blur.

The usual method to visualize and describe solid state transport is the electron band structure.

The first degree approximation - (nearly) free electron model - is to ignore atoms altogether and consider the volume as being filled with a homogeneous "charge gas". This is valid for metallic conduction because the conduction electrons are so "blurred" that they are oblivious to atomic positions and instead just have some abstract coupling to the lattice as a whole, e.g. to phonons.

From the 3d band structure, one can infer a conductivity tensor which provides the relation to the macroscopic quantities of voltage and current.

On the other extreme, the microscopic world, the band structure doesn't make extensive predictions and I think this is where your questions tried to pierce into. The formulation of the band structure paradigm is an attempt to simplify all the symmetries and redundancies that appear when you pour a huge number of electrons into a solid-state system and express it in terms of just a few mean-field quantities.

One microscopic prediction about individual conduction electrons at the Fermi level is that they move about incredibly fast, on the order of $10^6$ m/s (link). Without electric field, this movement is random, and even with a field, the directional drift is incredibly tiny (some 10-14 orders of magnitude weaker for usual current magnitudes). Maybe this example serves to show that conduction electrons don't nicely move on a ripply lattice underground but that it is a highly stochastic process.