Energy measurement of $W^-$ and $Z^-$ bosons

Question

$W$ bosons decay into an electron and electron-neutrino or into a muon and muon-neutrino. The $W$ lifetime is about $3 \cdot 10^{-25}\ \rm s$. That means the decay occurs close to the collision point, not in a detector.

The energy of the resulting electron or muon can be measured quite accurately, but for the neutrino the energy must be inferred (with a low accuracy).

How can one arrive at a precision like $80.385 \pm 0.015\ \rm GeV$ for the $W$ boson rest energy, as it is quoted in the literature?

(similar arguments apply to the $Z$)

Answer 1

The $Z$-boson mass is easily fully measurable since for e.g. the processes $Z\to e^+e^-$ and $Z\to\mu^+\mu^-$ the complete four-vectors $p_\mu$ of the two final state particles can be measured very precisely, and from this one can reconstruct the $Z$ four-vector and therefore its mass: $$m_Z^2=(p_1^\mu+p_2^\mu)^2$$

For the $W$ mass it is indeed a little more tricky: as you say, the neutrino cannot be directly measured, since it does not interact with the detector and only shows up as missing transverse energy ("MET"). Since at hadron colliders, we do not know what the momentum balance in the longitudinal direction is (beam remnants disappearing along the beam line, Lorentz boost due to unequal parton momentum fractions, etc.), we can only measure missing energy in the transverse plane, therefore for the neutrino we can only measure the transverse momentum $p_T^\nu$

The canonical method to determine the $W$-mass precisely at hadron colliders is to measure the so-called transverse mass, $m_T$. The spectrum of the transverse mass has a very visible feature often called the Jacobian Peak, at the point $m_W$.

$m_T$ is defined as $$m_T = \sqrt{2p_{T}^{l}p_{T}^{\nu}(1-\cos\Delta\phi_{l\nu})},$$

where the $\Delta\phi_{l\nu}$ is the angle in the transverse plane between the lepton and the direction of the missing transverse energy.

The resulting histogram from the recorded data is fitted with a line-shape that has $m_W$ as a floating parameter.

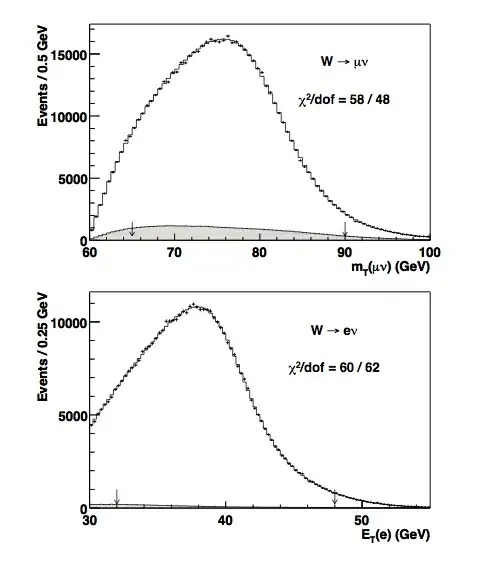
(from https://arxiv.org/abs/1203.0275)

Answer 2

I'm a little shakey on this history, but I believe the weak boson masses were first measured to high precision in electron-positron collisions. This allows you to know the precise initial state kinematics.

You look for events in which all the particles other than the $W$ are charged and were reconstructed in the detector then reconstruct the four momentum of the $W$ through conservation of momentum.

In a lepton collider you can do this exactly because you know the four momenta of the input particles exactly. In a hadron collider this is more difficult because at the vertex level the collision was between two partons (quarks or gluons) rather than between (say) two protons. This means you only know the input kinematics up to two momentum fractions. Meaning that you have to rely on Monte Carlo to understand the distribution of the transverse masses.

I think anna v was around while these measurements were hot new science and can probably provide a detailed description.

---

The 2012 Particle Data Book has a chapter on exactly this question (PDF link). To quote

In the $e^+e^−$ collider (LEP) a precise knowledge of the beam energy enables one to determine the $e^+e^− \to W^+W^-$ cross section as a function of center of mass energy, as well as to reconstruct the W mass precisely from its decay products, even if one of them decays leptonically.

and

Production of on-shell $W$ bosons at hadron colliders is tagged by the high $p_T$ charged lepton from its decay. Owing to the unknown parton-parton effective energy and missing energy in the longitudinal direction, the collider experiments reconstruct the transverse mass of the $W$, and derive the $W$ mass from comparing the transverse mass distribution with Monte Carlo predictions as a function of $M_W$.

Of the two contributions (lepton and hadron machines) the hadrons win out in the end (I suppose due to their huge luminosities).

---

Aside: the $Z$ is easier by far because it can decay into a pair of charged leptons (about 3% of events go to $\mu^+\mu^-$ which is a experimenter's dream of a final state) allowing a precise reconstruction of the whole decay.