I am a high school student and I am confused in one thing:"Why do we always assume in problems that if things are initially in contact with each other then they would be like that always?"
1)Suppose we have two blocks(A and B) initially in contact with each other and we apply force "F" on block "A". At first, I used to think that the contact force between block A and B would rise to the point when they acquire the same acceleration and at this moment I thought they would move together so at this point the contact force would become constant as there is no "deformation-reformation" thing happening after this moment. But if that's the case then at this moment the velocity of block A would still be higher than block B because its initial acceleration was more. If I have to plot a curve of acceleration-time it would be something like this:
At first, I used to think that the contact force between block A and B would rise to the point when they acquire the same acceleration and at this moment I thought they would move together so at this point the contact force would become constant as there is no "deformation-reformation" thing happening after this moment. But if that's the case then at this moment the velocity of block A would still be higher than block B because its initial acceleration was more. If I have to plot a curve of acceleration-time it would be something like this: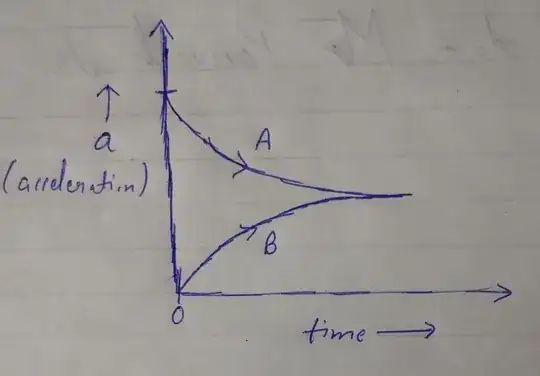 . the shape of the curve is random but I think it doesn't matter to my point(unless curve A crosses B and go even below it), the area under curve A would be higher than B so its velocity should be higher even at the moment when both have acquired the same acceleration. So, the deformation-reformation should still be happening as A is still approaching B and they would "never" reach to a common acceleration. So, why do we "assume" in problem solving that if these block are initially in contact, they would maintain that contact? But in reality, we have seen them moving together so how does this happen?
. the shape of the curve is random but I think it doesn't matter to my point(unless curve A crosses B and go even below it), the area under curve A would be higher than B so its velocity should be higher even at the moment when both have acquired the same acceleration. So, the deformation-reformation should still be happening as A is still approaching B and they would "never" reach to a common acceleration. So, why do we "assume" in problem solving that if these block are initially in contact, they would maintain that contact? But in reality, we have seen them moving together so how does this happen?
- This question came to my mind because I was thinking of a similar question of "water in a bucket revolving in a vertical plane" . We know that the water doesn't spill out from the bucket because the internal forces changes in a way so as to make the exact centripetal force required for water to move along with bucket. But the real question is: "How the internal forces "knows" that they have to maintain thing in contact at any moment in time?"
Please answer in simple language if possible. Or if its a difficult concept for a high school student to learn ,please answer only in brief and let me know.