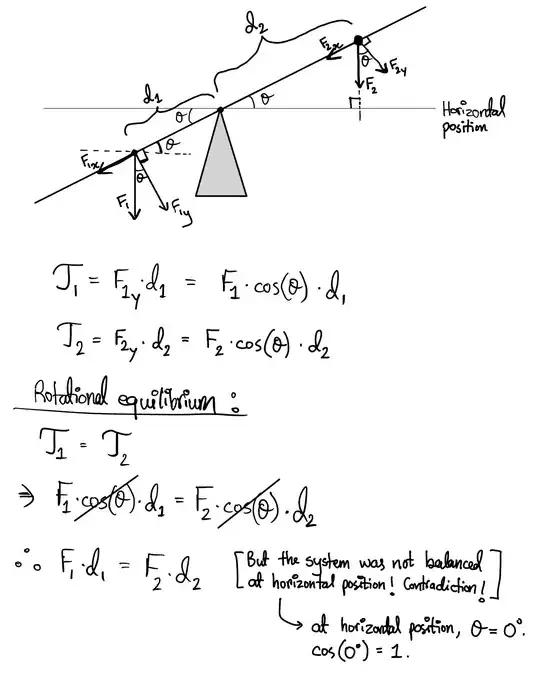
When discussing torques on a beam-balance (or see-saw) system, most textbooks focus on the requirements for the equilibrium of the system while being horizontal. However, I got interested in the following problem, but it seems like I have arrived at contradictory results:
Let two objects, with weights $F_1$ and $F_2$, be situated at opposite sides of the pivot at $d_1$ and $d_2$ distances from the pivot respectively. The pivot is at the center of gravity of the see-saw. Suppose that the system is not initially balanced at the horizontal position. We want to find out the angle at which this system rotates (towards the side with greater torque, of course) to arrive at equilibrium.
As you can see, I have considered the perpendicular components (with respect to the see-saw) of $F_1$ and $F_2$, and used them to find the torques while being tilted at an angle $\theta$. Since the tilted system is considered to be at equilibrium, the two torques (one clockwise and the other anticlockwise) must be equal. But, the $cos(\theta)$ cancels out and we arrive at a contradiction. Where is the problem?
I have found a similar (but not same) version of my problem at: Angular equilibrium on a see-saw
However, the setup of that system is a bit different. There, the pivot (center of gravity of the see-saw) is suspended and can rotate about a fixed point. The answer to that post seems reasonable to me, but my situation here is not exactly the same as that.
Any solutions or insights into my problem will be much appreciated. Thanks!