Angular equilibrium on a see-saw

Question

I have a tonne of questions related to see-saw equilibrium because most places I've been to online only deal with horizontal equilibrium - but static equilibrium can occur on an angle too. My questions stem from some torque/force concepts established in a previous question:

Why does the weighing balance restore when tilted and released

In the above link, it was established that by applying an unbalanced force to one side of the scales, they will begin to sink towards the side of the applied force. However, by doing so, the torque from the force is decreased (since only the component of the force perpendicular to the beam contributes to torque) - and apparently torque on the opposite side increases. Eventually a point will be reached where the two opposing torques are in equilibrium.

1. How can I calculate the angle of the 'beam' when equilibrium is reached?
2. How can I calculate the individual torque of both sides when the scales are in equilibrium. (I know they will be both equal, but how can I find them?)

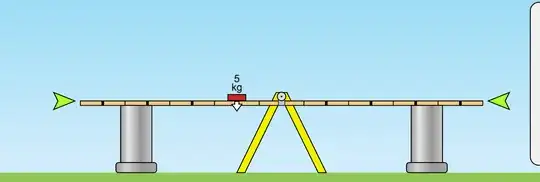
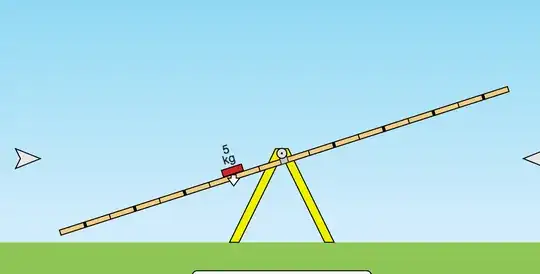
Also, could you help me see if the following way of conceptualising the situation is accurate: When a force is applied to only one side of some scales (or a see-saw, like in the image below), the centre of gravity is not initially at the pivot point....

So the see-saw will rotate about the pivot point until the centre of gravity occurs in the same location as the pivot point, where equilibrium is achieved (Is this true? I just assumed it).

p.s. images from a PhET simulation (:

Answer 1

If the see-saw is hanging from the pivot point, at equilibrium we would have the following situation:

The beam's overall length is $2L$ and is attached to the pivot point $P$ at the centre of the beam. I'll also assume the centre of gravity of the system is in $O$ ($mg$ is the total weight of the system: beam plus $PO$) and that the distance between $O$ and $P$ is $D$.

Three torques with the following absolute values act about $P$: $$|T_1|=F_1(L \cos \theta-D \sin \theta)$$ $$|T_2|=F_2(L \cos \theta+D \sin \theta)$$ $$|T_3|=mg D\sin \theta$$ At equilibrium: $$\Sigma T=0=|T_1|-|T_2|-|T_3|$$ $$F_1(L \cos \theta-D \sin \theta)-F_2(L \cos \theta+D \sin \theta)-mg D\sin \theta=0$$ $$(F_1-F_2)L\cos \theta=(F_1+F_2+mg)D\sin \theta$$ $$\tan \theta=\frac{F_1-F_2}{F_1+F_2+mg}$$ Note that if we start from $\theta \neq \theta_{equilibrium}$, then there is a net torque, say $T(\theta)$.

The equation of motion then becomes:

$$T(\theta)=I\frac{d^2\omega}{dt^2}$$ Where $I$ is the moment of inertia of the system about the point $P$ and $\omega$ the angular velocity of the CoG of the system about $P$. That's the equation of motion of an oscillation and for small angles $\theta$ of a simple harmonic oscillation. So the system will not simply move to equilibrium, it will oscillate about it.

Answer 2

In a NON-FRICTION environment the system will rotate in the direction of the side with higher torque until the arm is located directly beneath the pivot and the other arm is directly above the pivot. At that time, there is no net torque about the pivot and the system will again be in equilibrium.

Torque = Force applied x Distance from pivot

Use this article by NASA as reference. Read the part in italics at the bottom very carefully. No FRICTION is considered at the pivot.

The simulation by Phet includes some friction at the pivot. I have also created a similar but better version of the Balance and Torque Simulation in HTML5.

Answer 3

It looks like the pivot is slightly displaced from the beam's center of mass. If the center of mass of the beam is displaced slightly below the pivot by some distance $D$, then just pick the pivot as the center of mass and calculate the torque from that small displacement as the angle of the beam changes. The force $g\, M$ of the center of mass is downward, and it moves to the right by $D \sin \theta$ when the beam tilts at angle $\theta$, so the torque due to that is just $g\, M\, D \sin \theta$.

The torque from the 5kg mass must be equal and opposite. If the smaller mass $m$ is a distance $d$ from the center of the beam, then the torque is approximately $g\, m\, d \cos\theta$ -- or more precisely $g\, m\, \sqrt{d^2 + D^2} \cos [\theta + \arccos(D/\sqrt{d^2 + D^2})]$. To get the second form here, you just use the magnitude of the force ($g\, m$) times the distance between the pivot and where that force is applied ($\sqrt{d^2 + D^2}$, which is the hypotenuse of the little triangle with legs $d$ and $D$) times the sine of the angle between $\vec{r}$ and $\vec{F}$ -- or equivalently the cosine of $90^\circ$ minus that angle. Now, when the beam is level that angle is $90^\circ - \arccos(D/\sqrt{d^2 + D^2})$, which you can see by looking at that triangle again. And as you tilt the beam, you just increase the angle (decreasing the torque).

I also want to add a more general comment about torque. Calculations with torque are really easy (especially in equilibrium), but students frequently forget the most important thing to do in such calculations: pick an origin and stick with it. You can pick any origin at all, and the calculation should come out right. Just be sure to use the same origin for all the torques you use.

Even though any origin should work, there is one little trick to choosing the origin that can make things easier. Depending on where you choose your origin, certain hard-to-calculate things may cancel out. Now, remembering that torque is $\vec{r} \times \vec{F}$, you'll want to choose an origin where $\vec{r}=0$ for some force, or the force is perpendicular to $\vec{r}$, for as many of the forces as possible.

In your example, choosing the origin somewhere along the beam makes it at least easier to calculate the angles. One natural choice would be at the pivot point, because $\vec{r}=0$ for that force, so there would be no force from the pivot. But you could also choose the origin at the location of the mass, in which case you would need the force of the pivot.

Now, you may be concerned that you have no information about the force exerted by the pivot. But you can make another equation that will tell you it. The sum of the torques must be zero in equilibrium, but the sum of the forces must also be zero in equilibrium. This looks like a harder way to solve the problem in this particular case, but there are other cases where it can be useful.