I would like to understand why there's a $\nu²$ in the expression of the equivalent Young modulus in the Hertzian contact theory.
Here's a common expression for an elastic sphere crushed on a rigid plate: $\frac{E}{1-\nu²}$.
Most of the book I rode didn't present any proof of the expression.
Thank you in advance.
General appeals to Hooke's Law, Poisson effects, and plane-stress or plane-strain states seem too hand-wavy to address this precise question: How, exactly, does the $\frac{E}{1-\nu^2}$ term arise?
To restate and frame the question, if the end of an elastic rod or bar (with Young's modulus $E$) is pressed against a rigid plane, the effective stiffness (related to the force $F$ required for a given displacement $\delta$) is $E$. (Specifically, $\delta=\frac{FL}{EA}$ for a bar cross-sectional area of $A$.) OK, no surprise there.
In contrast, if a sphere of the same material with radius $R$ is pressed against the plane, the effective material stiffness term is $\frac{E}{1-\nu^2}$, where $\nu$ is the material Poisson's ratio. (Specifically, $\delta=\left(\frac{9F^2}{16R}\right)^{1/3}\left(\frac{1-\nu^2}{E}\right)^{2/3}$, as discussed in Johnson's Contact Mechanics, for example.) Poisson's ratio appears because the contact diameter is narrower than the sphere diameter; the effective stiffness term is larger ($E/(1-\nu^2)>E$) because material adjacent to the contact area has "gotten in the way" of the displacement—a situation that doesn't arise in the case of the uniformly compressing rod. Poisson effects involve lateral displacement or constraint, so it's natural that $\nu$ appears in some way here. (Compare the biaxial modulus, which represents the increased stiffness of a compressed film because it can't expand in the lateral directions.) But this doesn't explain the exact form of $\frac{E}{1-\nu^2}$.
It's straightforward to trace the $\frac{E}{1-\nu^2}$ term back to a certain point: the vertical displacement in the region under and around a point load applied to the surface of a semi-infinite region (sometimes called a half space):
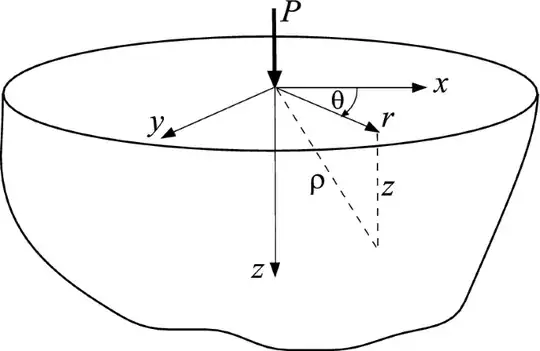
The connection between the point load and the indenting sphere is (1) the sphere displacement given above is valid only for small contact areas (thus, the sphere surface over such a small area is essentially as flat as a plane) and that (2) any arbitrary vertical pressure load can be decomposed into individual point loads.
The vertical displacement $\delta$ (as reported in many discussions of the so-called Boussinesq problem: example, example, example) is
$$\delta=\frac{F}{4\pi G}\left[\frac{2(1-\nu)}{\rho}+\frac{z^2}{\rho^3}\right],$$
where $G$ is the shear modulus, $\rho=\sqrt{x^2+y^2+z^2}$ is the 3-D distance to the point of load application, and $z$ is the depth from the surface. Note that $G=\frac{E}{2(1+\nu)}$. Thus, at the surface,
$$\delta=\frac{F}{\pi\rho}\left(\frac{1-\nu^2}{E}\right),$$
which provides the desired term $\frac{E}{1-\nu^2}$. (The singularity at $\rho=0$ is eliminated by integrating over a finite contact area.)
So how is the displacement calculated? Unfortunately, although many solutions exist, I don't know of one simple enough to summarize in an answer here. (The simplest expression I could devise would be something like "The appropriate Papkovich–Neuber potentials that satisfy harmonic and compatibility constraints contain the term $1-\nu$, which when the shear modulus is converted to Young's modulus leads to $\frac{E}{1-\nu^2}$.")
Again, Boussinesq is credited with the first published solution (in 1885). Love reviewed the solution in A Treatise on the Mathematical Theory of Elasticity (1944). An alternative approach appears in Popov et al.'s Handbook of Contact Mechanics. Yet another appears in Apostol's "Elastic equilibrium of the half-space revisited: Mindlin and Boussinesq problems". See also Ike's "General solutions for axisymmetric elasticity problems of elastic half space using Hankel transform method" and the same author's "First principles derivation of a stress function of axially symmetric elasticity problems, and application to Boussinesq problem". (In fact, you might wish to contact Prof. Ike for his thoughts on the original question.) Many other solution methods lie behind paywalls. On the topic of simplicity, see The “Quick and Dirty” Way to Derive Boussinesq’s Point Load Stress Equations.
I'm hopeful that this answer can be supplanted by a simpler one and have offered a Physics Stack Exchange bounty accordingly.
Contact normal force is proportional to "directional Young's modulus" :
$$ F_{_N} \propto \frac {E}{1-\nu ^{2}} ,$$
Basically, it means that material can respond back with strong normal force, either if it has high stiffness or high Poisson ratio, meaning that material can accumulate deformation in perpendicular directions of applied crushing force, and then "release it back". This process is best seen from picture :
