If I have a bipartite system of two qubits $A$ and $B$, and the density matrix $\rho$ is separable, how do I decompose it into its separable parts?
That is, give $\rho$, expand it as follows:
$$\rho = \sum_{i=0}^Np_i \ \rho_{i}^A \otimes \rho_{i}^B $$
Where $0 \le p_i \le 1$ and $\rho^{A,\ B}_i$ are density matrices on the two subsystems $A$ and $B $ for some $N$.
I also found myself interested in this problem and what seemed like a lack of discussion on how to tackle it (as pointed out in the comments it is, computationally, a very hard problem in general).
In the literature a most significant contribution came from Lewenstein and Sanpera in 1998 with a Letter proving that for any density matrix $\rho$ and set $V$ of product vectors belonging to the range (i.e. rowspace) of $\rho$ there exists a best separable approximation (BSA) of the matrix in the sense $\rho=\rho_s^*+ \delta \rho$ where $\rho_s^*$ is separable and the trace $\text{Tr}\delta \rho$ of the entangled part is minimised.
They also provided an explicit construction for the separable part. The idea is to generate a large set $V$ of projectors $\lvert \alpha \rangle \langle \alpha \rvert$ randomly chosen from $\text{Range}(\rho)$ and seek a decomposition $\rho_s^*=\sum_{\alpha\in V} \Lambda_\alpha \lvert \alpha \rangle \langle \alpha \rvert$ where the $\Lambda_\alpha \geq 0$ are pairwise maximised: $(\Lambda_{\alpha_1} \lvert \alpha_1 \rangle \langle \alpha_1 \rvert + \Lambda_{\alpha_2} \lvert \alpha_2 \rangle \langle \alpha_2 \rvert) $ should be the largest contribution that can subtracted from $\rho$ whilst retaining the non-negativity of the difference $(\dagger)$.
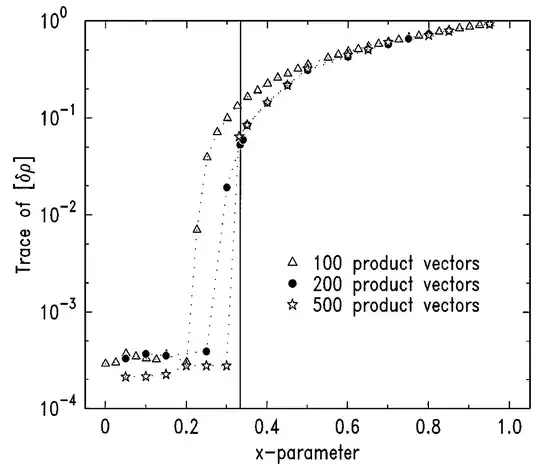
Lewenstein and Sanpera include explicit expressions for the $\Lambda_\alpha$, but in practice resort to trial-and-error (i.e. brute force) to sidestep potential issues of convergence here. Below is the one figure from their Letter showing the trace of the residual (non-separable) part when applying this approach to a $2\otimes2$ Werner state $\rho_w(x)$ known to be separable for values of the parameter $x\leq 1/3$. The upshot is that, provided the number of product vectors chosen for $V$ is sufficiently large, the result does not depend on this number and the true BSA is obtained (the non-zero part seen for $x\leq 1/3$ is a result of the numerical precision set to $10^{-4}$ here).
That's the general problem; following a brief flurry of activity after the Lewenstein-Sanpera result (the "Lewenstein-Sanpera" decomposition) I could not find much further work for arbitrary density matrices. However, there has been a great deal of progress for specific cases (Edit: as kindly pointed out in the comments, this includes extensive work in the domain semidefinite programming for bipartite states and hardness). In particular the problem you describe, that for two qubits, does in fact have a closed form solution.
The clearest presentation of this I could find is by Jafarizadeh et al. (2005) who rather elegantly show that the problem can be formulated as one of semidefinite programming and proceed to derive the best separable approximation of a generic two qubit density matrix using the Wootters basis $\{\lvert x_i \rangle\}$ for $\rho$ $\displaystyle({\dagger\dagger})$. In the case $\rho$ is separable this reduces to $\rho=\rho_s$ where $$ \begin{align*} \rho_s = ( \lambda_2+\lambda_3+\lambda_4 ) \lvert x_1' \rangle \langle x_1' \rvert + \lambda_2 \lvert x_2' \rangle \langle x_2' \rvert + \lambda_3 \lvert x_3' \rangle \langle x_3' \rvert + \lambda_4 \lvert x_4' \rangle \langle x_4' \rvert \end{align*} $$ is in fact a separable matrix. Here $\lambda_i$ are the squares roots of the eigenvalues in decreasing order of the non-Hermitian matrix $\rho \tilde{\rho} $, with $$ \tilde{\rho} = (\sigma_y \otimes \sigma_y) \rho^* (\sigma_y \otimes \sigma_y),$$ and $\lvert x_i'\rangle=\lvert x_i \rangle /\sqrt{\lambda_i}$ are the Wootters states scaled by the square root of these values.
$(\dagger)$ e.g. For a single $\Lambda_\alpha$ this means $\rho- \Lambda_\alpha \lvert \alpha \rangle \langle \alpha \rvert \geq 0$ and for every $\epsilon\geq0$, $\rho-\Lambda_\alpha \lvert \alpha \rangle \langle \alpha \rvert $ is not positive definite.
$(\dagger\dagger)$ This is a (non-separable) decomposition $\rho=\sum_i \lvert x_i \rangle \langle x_i \rvert$ shown by Wootters (also in 1998) to always exist.
