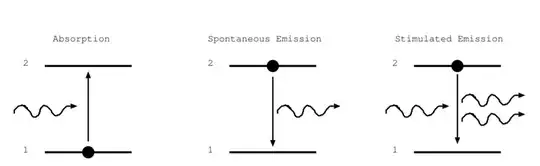
Einstein coefficients for emission and absorption ($A_{21}$, $B_{12}$, $B_{21}$) are often derived from a consideration of thermodynamic equilibrium using Boltzmann statistics and comparison with Planck's law. This (among many others) is the typical approach: https://www.youtube.com/watch?v=4TOvjtovRXY
How can it be that intrinsic microscopic properties (which might be calculated by quantum mechanics on n-level systems including radiation fields) can be derived so "easily" based just on thermodynamics, which is itself of rather statistical nature?
I've always seen some kind of deep miracle behind this derivation: What is the right way to understand it? Einstein, at this time (1917), had no idea about how quantum mechanics would look like in about one decade in the future - how is it possible, that he got somehow a valid relation without doing complicated quantum mechanical calculus on the atomic level? Isn't that great?