I know there are many similar analysis about this topic, like here, here, many of them are answered by Qmechanic, excellent answer!
I have checked most of these posts, but I still don't clearly understand something. So I want to organize this question in my way. If there is a duplicate, I apologize.
All of my following statements and conventions based on Peskin and Schroeder's QFT book.
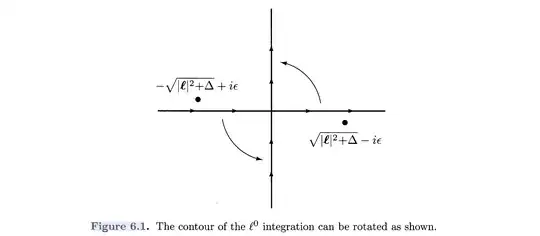
Begin with their book on page 192, the book gives a figure about wick rotation, and defined the Euclidean 4-momentum variable $\ell_E$ in (6.48) $$\ell^0 \equiv i \ell_E^0 ; \qquad \vec{\ell}=\vec{\ell}_E. \tag{6.48}$$
My first question is, why does $\ell^0 \equiv i \ell_E^0$ imply this counterclockwise rotation. In my understanding, $\ell_E^0$ is the vertical line in the figure, goes from bottom to the top. $\ell^0$ is the horizontal line from left to right. And $\ell_E^0=-i\ell^0$ implies that this rotation is a clockwise rotation from $II$ and $IV$'s region, which cross the poles.
On book page 293, the book defined the Wick rotation of time coordinate: $$t\rightarrow -ix^0. \tag{9.44} $$ This seems reasonable to me.
If we want to transfer the two-point correlation function from Minkowski space to Euclidean space, which corresponds to eq.(2.59) and (9.48) $$D_F(x-y) \equiv \int \frac{d^4 p}{(2 \pi)^4} \frac{i}{p^2-m^2+i \epsilon} e^{-i p \cdot(x-y)}, \tag{2.59}$$ $$\left\langle\phi\left(x_{E 1}\right) \phi\left(x_{E 2}\right)\right\rangle=\int \frac{d^4 k_E}{(2 \pi)^4} \frac{e^{i k_E \cdot\left(x_{E 1}-x_{E 2}\right)}}{k_E^2+m^2}. \tag{9.48} $$ I have tried to use eq.(6.48) and (9.44) to derive out (9.48) from (2.59), but I find they have a minus sign difference between the time component, in other words, I got: $$\left\langle\phi\left(x_{E 1}\right) \phi\left(x_{E 2}\right)\right\rangle=\int \frac{d^4 k_E}{(2 \pi)^4} \frac{e^{-i k_E^0 \cdot\left(x_{E 1}^0-x_{E 2}^0\right) + i \mathbf{k_E}\cdot \left(\mathbf{x_{E 1}-x_{E 2}}\right)}}{k_E^2+m^2}. $$ So which is correct?
The above three points are my confusion about Wick rotation, could you (Qmechanic) and other people, please elaborate more about this, thanks!