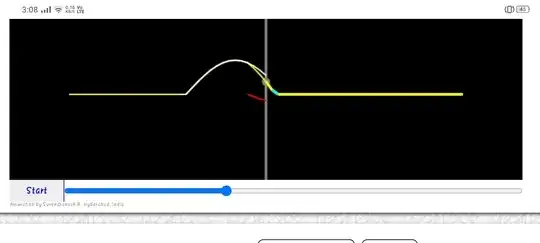
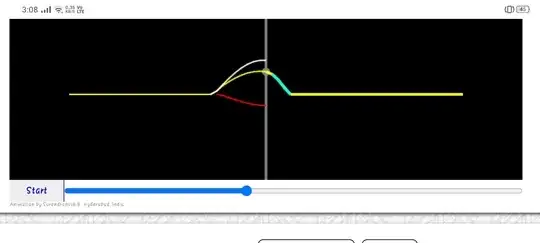
Short answer
It follows from the algebraic conditions governing interface condition at the interface between the two media, with linear behavior.
Details
You can think at the problem as the union of the problems in two neighboring media and a common boundary. Let's call medium 1, the medium where the original incident wave is traveling and reflection occurs, and medium 2 where the transmission occurs. Medium 1 is in the region of space $M_1: x \in [x_1, x_i]$, medium 2 in $M_2: x \in [x_i, x_2]$, where $x_i$ is the position of the interface.
Interface conditions. What happens in the media depends on the common boundary surface, and what happens on both sides of the boundary is governed by interface conditions (coming from integral balance equations, for an elementary volume across the interface surface). As an example, the electric field on a interface with no charge surface density is constant across the surface
$\mathbf{e}_1(x_i,t) = \mathbf{e}_2 (x_i,t)$.
At the medium interface, usually an algebraic condition holds to determine the transmission and reflection ratio, namely
$i_t = 1 + i_r,\qquad$ with $i_t \in (0,1)$,
that quantifies the amount of the signal transmitted in medium 2 and the amount of signal reflected, as fraction of the incident signal.
Solution as superposition of traveling waves. The field in medium 1 is the superposition of the incident and the reflected wave, while field in medium 2 come from the transmitter wave only
$e_1(x, t) = e_i(x,t) + e_r(x,t) = e^{t.w.}_i(x-v_1t) + e^{t.w.}_r(x+v_1t)$
$e_2(x, t) = e_t(x,t) \qquad \qquad \ = e^{t.w.}_t(x-v_2 t)$,
having written them explicitly as traveling waves. Now we can write the three contributions as:
- incident wave: its value at the interface is $e^{t.w.}_i(x_i -v_1 t)$.
- transmitted wave: its at the interface is
$e^{t.w.}_t(x_i - v_2 t) = i_t e^{t.w.}_i(x_i - v_1t) $,
- reflected wave: its at the interface is
$e^{t.w.}_r(x_i - v_2 t) = i_r e^{t.w.}_i(x_i - v_1t) =
(i_t - 1) e^{t.w.}_i(x_i - v_1t)$,
so that both the interface condition $e_1(x_i, t) = e_2(x_i, t)$ and the ratio of the transmission and reflection signal are satisfied.
Properties of traveling waves.
Now, we only need to reconstruct the full signal in the media, knowing that its made of traveling waves and knowing the boundary conditions. For a "backward" traveling wave, we know that
$f(x_0,t_0) = f^{t.w.}(x_0+vt_0) = f^{t.w.}(x_1+vt_1) = f(x_1,t_1)$,
if the argument of the traveling wave is the same, i.e.
$x_0 + v t_0 = x_1 + v t_1$$\qquad \rightarrow t_1 = t_0 + \dfrac{ x_0 - x_1}{v}$,
while for a "forward" traveling wave $t_1 = t_0 - \dfrac{ x_0 - x_1}{v}$.
Solution of the problem.
Putting everything together, we can write the solution of our problem. The field in medium 1 reads
$e_1(x,t) = e_i(x,t) + e_r(x,t) = \\
\qquad \ \ \ = e^{t.w.}_i(x-v_1t) + e^{t.w.}_r(x+v_1t) = \\
\qquad \ \ \ = e^{t.w.}_i(x-v_1t) + e^{t.w.}_r\left(x_i, t - \dfrac{x_i-x}{v_1}\right) = \\
\qquad \ \ \ = e^{t.w.}_i(x-v_1t) - (1-i_t) e^{t.w.}_i\left(x_i, t - \dfrac{x_i-x}{v_1}\right) = \\
\qquad \ \ \ = e^{t.w.}_i(x-v_1t) - (1-i_t) e^{t.w.}_i\left(x, t - 2\dfrac{x_i-x}{v_1}\right) \\
\qquad \ \ \ = e^{t.w.}_i(x-v_1t) - (1-i_t) e^{t.w.}_i\left(x -v_1 \left( t - 2\dfrac{x_i-x}{v_1} \right) \right) \\
\qquad \ \ \ = e^{t.w.}_i(x-v_1t) - (1-i_t) e^{t.w.}_i\left(-x -v_1 \left( t - 2\dfrac{x_i}{v_1} \right) \right) \\$
while the field in medium 2 reads
$e_2(x,t) = e_t(x,t) = \\
\qquad \ \ \ = e^{t.w.}_t(x-v_2t) = \\
\qquad \ \ \ = e^{t.w.}_t\left(x_i, t - \dfrac{x-x_i}{v_2}\right) = \\
\qquad \ \ \ = i_t e^{t.w.}_i\left(x_i, t - \dfrac{x-x_i}{v_2}\right) .$
Harmonic signals.
Assuming the incident signal is an harmonic signal, $e^{t.w.}_i(x-v_1 t) = A e^{i k_1(x-v_1t)} = A e^{i (k_1x-\omega_1 t)}$, with $\omega_1 = \dfrac{v_1} k_1$,
the solution reads
$e_1(x,t) = A e^{i (k_1x-\omega_1 t)} - (1-i_t) A e^{i \left(-k_1 x -\omega_1 \left(t -2\frac{x_i}{v_1} \right) \right)} =
e^ {i \omega t} \left[ A e^{i k_1 x} - (1-i_t) A e^{i \left(-k_1 x + 2 \omega_1 \frac{x_i}{v_1} \right) } \right]$
$e_2(x,t) = i_t A e^{i \left(k_1 x_i -\omega_1 \left( t - \frac{x-x_i}{v_2} \right) \right) } =
e^{-i \omega_1 t} \left[ i_t A e^{i \left(k_1 x_i + \omega_1 \frac{x-x_i}{v_2}\right)} \right]
$,
that clearly shows that, at every point in space, the signal has the same time frequency $f_1 = \dfrac{\omega_1}{2\pi}$.