Where did I go wrong with quantum photon polarization?

Question

J Murray answered a previous question with a proof of Bell's Inequality, and a description of it applying to photon polarization.

I probably misunderstood the application to photons, so I want to get that clearer.

First, I think I misunderstood the description of games where the two grad students try to maximize the correlation. They can't be allowed to communicate, or else the experiment could be done while they're at lunch and both filters are set at zero the whole time. Their own settings have to be uncorrelated, so they can be treated as independent random variables.

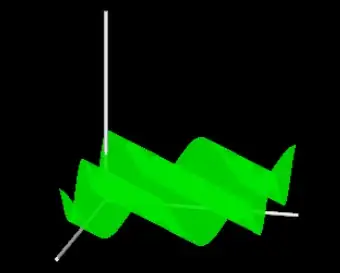
So what I should do is, for every combination of filter x angle and filter y angle, integrate over angle $\theta$ for the entangled photons, and graph the result.

Next, what I see is relevant about entangled photons, is that they they must have either the same result from a polarizing filter, or the opposite result. I don't care which. So if one particular entangled photon is 100% certain to get through a particular filter, then its entangled photon is either 100% certain to get through, or 100% certain to be absorbed.

So if a photon has a state $\lambda$ that includes a linear polarization angle $\theta$, then its entangled photon has state $\lambda'$ which includes polarization $\theta$, or $\theta+-\pi$, or $\theta+-\pi/2$.

I will start out with the first case because it's easier for me to think about, but maybe in real examples entangled photons are always opposite.

What if entangled photons encounter a filter that is not at 0 or $\pi/2$ or $\pi$ etc? Say the angle is at $\pi/6$ relative to the photon's polarization. Then we know one entangled photon has probability 3/4 to get through. What about the other one?

If all they have in common is their polarization angle, then the second photon will also have 3/4 chance to get through, and for both it's 9/16. 5/8 for both or neither, 3/8 that one gets through, 1/16 neither gets through,.

But maybe if one gets through then the other one must also. Then their combined probability is 3/4, and the probability that neither gets through is 1/4.

Or it could be anywhere in between. Maybe half of them are destined to get through, and for the other half it's an independent 1/2 chance. So 5/8 both get through, 1/4 one does, and 1/8 neither does.

Starting with the idea that entangled photons have independent chances to get through filters, I graphed the probability that both get through, given x and y.

You can look at the 3D graph if you like. Hold down the right button and move the mouse to rotate it.

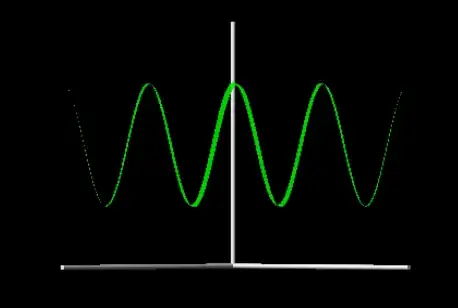
The results are the same depending on x-y. It's a cosine wave with minima at 1/8 and maxima at 3/8, average 1/4.

The graph for both absorbed is the same, so their sum has average 1/2 with minima at 1/4 and maxima at 3/4.

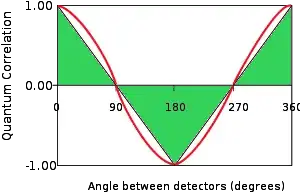
This looks similar to the intuitive picture.

They simplified it to make the zeroes at 90 degrees and 270 instead of 45, 135, 225, and 315. Also their maximum is at 1 instead of .75. But their argument that it should be straight lines and not a sine wave would probably apply. Why is it a sine wave?

I looked at Araujo's explanation and found only one possible reason to expect that it shouldn't be.

$$p(ab|xyλ)=p(a|xλ)p(b|yλ)p(λ)$$

But this is not true for light. The closer x and y are, the more highly correlated a and b are. And when $p(a|x)$ and $p(b|y)$ are correlated, we can't expect $p(ab|xy)=p(a|x)p(b|y)$.

The conditions for this explanation of Bell's Theorem are not met by light, regardless whether entangled photons do something peculiar.

So I think the simple picture explanation is wrong. Also Araujo's explanation does not fit classical explanations for light, unless I misunderstand it. A classical description of light does not fit the assumptions which lead to Bell's Inequality. (Though Bell's Inequality could still be true for it.)

Where did I go wrong?

Answer 1

Unless I am misunderstanding the diagram, your setup seems to be still very classical and has nothing to do with Bell's theorem.

Bell's theorem concerns entangled photons. You write:

Say that we have two filters α and α that are set to the same angle. We send linearly-polarized photons through them, both with angle θ precisely π/4 different from the filters' angle

The two polarizers have the same angle (more on this next). Let us choose the polarizer position as our basis, let's say $|\updownarrow\rangle$ and $|\leftrightarrow\rangle$, for parallel and perpendicular to the polarizers, respectively. The photons are at a $\pi/4$ angle, so the state of a single photon can be written as $|\pi/4\rangle =\frac{1}{\sqrt2}(|\updownarrow)+|\leftrightarrow \rangle)$. If the two photons are polarized in the same direction we have: $$|\pi/4, \pi/4 \rangle =|\pi/4\rangle\otimes| \pi/4 \rangle $$ $$=\frac{1}{2}(|\updownarrow\updownarrow \rangle+|\updownarrow\leftrightarrow \rangle+|\leftrightarrow\updownarrow \rangle+|\leftrightarrow\leftrightarrow \rangle)=\frac{1}{2}(|\updownarrow\rangle+|\leftrightarrow \rangle)\otimes(|\updownarrow\rangle+|\leftrightarrow \rangle),$$ which clearly shows that no matter in which basis you write it can be factored as the product of two single photon states. By definition a separable state is NOT an entangled state. If you were trying to prove some property of entangled states then the setup is not about that.

Back to the polarizers. Bell's theorem as shown in the picture of the previous post, shows when the quantum correlations violate the classical bound set by Bell:

The red line are the quantum correlations. Green are the correlations that are allowed by a local-hidden value theory. The bottom axis is the angle between the two detectors. Notice that if the angle is 0 (detectors at the same angle), the quantum correlations are in the local-hidden values region and can be thus explained classically.

With these two ingredients in mind, there are many ways to reproduce the results of this setup with classical experiments. With ANY of the two conditions above (non entangled photons or same angle polarizers) it is not possible to violate Bell's inequalities.

Answer 2

Why is it a sine wave?

The curve in the graph you posted is actually a cosine. This is the correlation between what is detected at the polarising detectors if the entangled photons are prepared with the same polarisation orientation. If the photons were prepared with orthogonal orientations, the correlations would be represented by a sine wave. A correlation of 0 means there is no correlation and the results are random. A correlation of -1 means perfectly anti-correlated, so when a photon is detected at A it is not detected at B and vice versa. The probability that a photon is detected at both A and B is the square of the correlation, so we get the probability as $cos^2(A-B)$ which is related to Malus' law as depicted below:

Also their maximum is at 1 instead of .75.

That is as it should be. If the entangled photons have been prepared so that their polarisations are aligned with each other, then if the detectors are also aligned with each other the correlation should be 1 and the probability of getting the same result is 100%. Note that we never get negative probabilities due to the squaring (which is a good thing).

I graphed the probability that both get through, given x and y

You have not defined what x and y are and the link to the 3D graph is not working for me so I cannot look at the code. However I suspect x and y are the orientations of the respective detectors. It is not really necessary to produce a 3D graph, because you can use the difference between x and y as a single variable and just plot a 2D graph, which is a bit easier to visualise.

The quantum prediction of a correlation of $\cos(A-B)$ is what is actually measured in labs, if the entanglement is not broken. This is what you have to match with any alternative theories. What Bell said was no local realist theory can match the quantum prediction. This does not rule out non-realist theories such as invoking infinite parallel universes being created every nanosecond or invoking super-determinism.

Quantum mechanics predicts two photons that are entangled behave as if they are single photon that is spread over a large distance. When the pair are passed through their respective polarising analysers, they behave the same as a single photon that passes through polariser A and then polariser B in succession (or vice versa - the order does not matter). This is why the probabilities of the correlations are the same as predicted by Malus' law.

Answer 3

It sounds like you are under the impression that we are making repeated measurements of a given photon, which is not right. The idea is that we have a pair of photons (for example, which may have been produced in an annihilation event) which are sent to two different detectors whose filter angles may be set independently.

The correlation being measured is between the readings of the two detectors which, again, are detecting separate photons. Each individual measurement appears to be random (we don't know a priori whether a given photon will be detected or not) but the readings on the detectors may be correlated. One might imagine that every time detector $X$ registers a photon, detector $Y$ also registers a photon and vice-versa, so the results are perfectly correlated $(C=+1)$. Alternatively, one might imagine that every time detector $X$ registers a photon, detector $Y$ fails to register a photon and vice-versa, so the results are perfectly anticorrelated ($C=-1$).

The point of the Bell theorem is that if the apparent randomness is due to the presence of a local hidden variable, then the correlations corresponding to the different detector settings (which are chosen at will by the experimenters before each trial) cannot be completely arbitrary; they must be constrained by a Bell inequality.

The inequality does not set a limit on the correlation between measurement results for any particular choice of detector settings - instead, it constrains how the correlations may vary as we turn the knobs on our detectors. It turns out that if the photons are entangled, then the Bell inequality is generally violated, ruling out a local hidden variable as the cause of the apparent randomness.