Non-distributivity of quantum logic according to C. Piron

Question

I'm trying to understand this highlighted sentence in Piron's "Foundations of Quantum Physics" on p. 21:

I know that distributivity of a lattice means $a\land (b\lor c)=(a\land b)\lor(a\land c)$ and $a\lor (b\land c)=(a\lor b)\land(a\lor c)$. But I don't know what (2.4) and (2.5) has to do with the lattice structure.

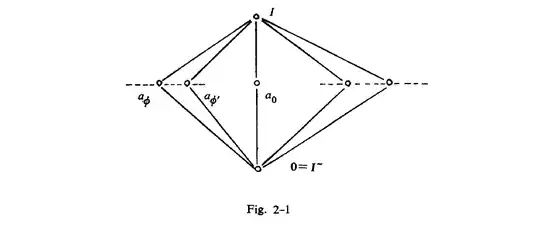
On the next page Piron draws this diagram for the lattice:

I also don't understand this. Since $a_\Phi < a_{\Phi\, \text {or} \,\Phi'}$ and $a_\Phi' < a_{\Phi\, \text {or} \,\Phi'}$, we can infer that $a_\Phi\lor a_{\varphi'} < a_{\Phi\, \text {or} \,\Phi'}\neq I$. Isn't it? What am I missing?

Explanation

In (2.4) and (2.5) above, $b$ and $c$ are propositions about a quantum mechanical system. The propositions are the equivalence classes of questions about that system described below.

The logical value of a question depends on the state of the system. By definition, the logical value of the question is true if any experiment performed in this state is affirmative. We introduce a transitive and reflexive relation $<$ between questions $\alpha$ and $\beta$ where $\alpha<\beta$ means that in any state when $a$ is true, $b$ is also true. The questions $\alpha$ and $\beta$ are regarded equivalent if both $\alpha < \beta$ and $\beta<\alpha$ holds. The equivalence classes of questions (the propositions) constitute such a partially ordered set $\mathscr L$ in which any pair of elements $a\in \mathscr L$ and $b\in \mathscr L$ has a least upper bound $a\lor b$ and a greatest lower bound $a\land b$. The structure $(\mathscr L,\lor,\land)$ is a lattice, since $\land$ and $\lor$ are associative, commutative and idempotent and both are absorptive against the other: $a\land (a\lor b)=a$ and $a\lor(a\land b)=a$

My thoughts about this issue

Let $b= the\, polarizer\,with\,angle\, \beta \ always\, \,transmits\, the\, photon$ and $c= the\, polarizer\,with\,angle\, \gamma \ always\, \,transmits\, the\, photon$

The notation in fig 2. would be $b=a_\beta$, $c=a_\gamma$.

Don't forget, $\lor$ desn't mean $or$. It is the lower upper bound of $b$ and $c$. Formulating in words, $b\lor c$ is the proposition "it is always true that the polarizer with angle $\beta$ or the polarizer with angle $\gamma$ transmits the photon. In the superposition state of state belong to $b=true$ and the state belong to $c=true$ , $b = false$, $c = false$ and $b\lor c = true$.

Then taking a proposition $a = true$,

$a\land (b\lor c) = true$ but $(a\land b)\lor (a\land c)=false$

This means the absence of distributivity, so it's OK.

(This is evidently wrong, since $1\land b = b$, $1\land c = c$, so if $a=1$ then $(a\land b)\lor(a\land c)=b\lor c=1\land (b\lor c) = a\land (b\lor c)$. So the non-distributivity is still not clear to me.)

But this contradicts the schema in fig. 2-1.

Answer 1

The point is that if $\land$ and $\vee$ corresponded exactly to classical and and or, then they would be distributive simply because the classical operators are distributive. It does not follow from the small excerpt you've presented that it is specifically distributivity that fails here - this must follow from your specific definitions of $\land$ and $\vee$, not from the generic fact that they're different from and and or. Valter Moretti explains the non-distributivity of the lattice of quantum probabilities in terms of Hilbert space projectors in this answer, particularly addendum 1.

Answer 2

First of all, nowadays, one learns it logic courses that "truth" is a complex notion, and in particular that "truth" per se has no real meaning; only "truth within a certain domain of interpretation" has one. Therefore, a sentence like "$b$ is true" has to be interpreted in some way, and I hope it is in the way that I stated my answer below.

Moreover, in logic, when dealing with something to be thought as a "set of propositions" (such as a lattice, a Boolean algebra, etc.), it is kind of a subtelty to distinguish between formal equality of two formulas and some kind of equivalence between them. For example, when one tries to define logic in full rigor, one first defines strings of characters, and at this low level, for example, one can consider that $(a\wedge b) \neq a\wedge b$. The highest (on the scale of abstraction) level of equivalence is to say that two propositions $a$ and $b$ are equivalent if $a\Leftrightarrow b$ is provable, within some implicit logical framework. It turns out that for quite a number of logics, this equivalence is the same as semantic equivalence, for which two propositions $a$ and $b$ are equivalent if, within every possible domain of interpretation of the formulas, they are both true or both false. Since Piron talks about "truth" and "falseness", I guess that it is correct to interpret his claim as stating a sort of semantic equivalence.

Let $L$ be a set, $\wedge,\vee : L\times L \rightarrow L$. Call a map $t: L \rightarrow \{\top,\bot\}$ a truth assignment if $\forall a,b \in L,\ t(a\wedge b) = \top \Leftrightarrow t(a) = t(b) = \top$ and $\forall a,b \in L,\ t(a\vee b) = \top \Leftrightarrow \left(t(a) = \top \ \textbf{or}\ t(b) = \top\right)$.

We say that two elements $a,b \in L$ are semantically equivalent if for all truth assignment $t$, $t(a) = t(b)$. Note that in classical logic, semantic equivalence is the same as logical equivalence.

Proposition: For all $a,b,c \in L$, $a \wedge (b \vee c)$ and $(a\wedge b) \vee (a\wedge c)$ are semantically equivalent.

Proof: Just examine all the cases! I'll look at one case, as an example. Let $t$ be a truth assignment. Assume that $t(a \wedge (b \vee c)) = \top$. Then $t(a) = \top$ and either $t(b) = \top$ or $t(c) = \top$. Assume $t(b) = \top$. Then $t(a\wedge b) = \top$, then $t((a\wedge b)\vee (a\wedge c)) = \top$. We can argue similarly when $t(c) = \top$.

As for the diagram, it represents the lattice of propositions on a two-dimensional Hilbert space. One can assume that this space represents the system consisting in a single photon, and every nontrivial proposition is of the form "the photon goes out of the polarizer with some angle". If one denotes $a_\phi$ the proposition "the photon goes out of the polarizer with angle $\phi$", what does $a_{\phi\ or\ \phi'}$ mean? Should it mean "the photon goes out of the polarizer with angle $\phi$ when put in, or goes out of the polarizer with angle $\phi'$ when put in"? Such a proposition does not exist: for opposite angles $\phi$ and $\phi'$, such a proposition would be greater or equal than $a_\phi \vee a_{\phi'} = true$, so would be $true$. However, any photon that goes out of a polarizer with a different angle would sometimes, in one of the $\phi$ and $\phi'$ polarizers, not go out, so $a_{\phi \ or \ \phi'}$ cannot be a valid quantum proposition.

Answer 3

The key sentence in Plop's answer is the following:

$a_{\phi \ or \ \phi'}$ cannot be a valid quantum proposition.

And indeed, this is true. We can measure only with a polarizer set to angle $\phi$ or a polarizer set to angle $\phi'$, but not with both.

---

Starting from the beginning: for a given quantum mechanical system we have different physical quantities. For each physical quantity $\alpha$, there is a set $T_\alpha$ having its possible values. A question about the physical quantity $\alpha$ is always "Will the value of $\alpha$ fall in $S$?" where $S$ is a Borel subset of $T_\alpha$.

The proposition system (the logic of the given quantum mechanical system) consists of equivalence classes of questions (possibly about different physical quantities).

My failure was that I thought that here is about one single physical quantity with possible values $\phi\in \mathbb R/\pi$.

But I realized that I should have taken seriously that the polarization experiment is a yes/no experiment and that this means that there is a physical quantity for each $\phi$ with values in $T=\{0,1\}$. These quantities are incompatible with each other since we can measure the photon's polarization only once. If we measure in direction $\phi$ then we can't measure simultaneously in direction $\phi'\neq \phi \pmod{\pi}$. The lattice of the Borel subsets of $\{0,1\}$ is this: In the lattice of the whole proposition system, $\{0\}$ and $\{1\}$ is different for different $\phi$-s (since they aren't equivalent), but $\{0,1\}$ (the identical true question) and $\{\}$ (the identically false question) is common (since they are equivalent for different physical quantities). So the whole proposition lattice looks similarly to Piron's diagram, only the notation should be changed:

As for the highlighted sentence in the question, I've only just understood what ACuriousMind wanted to say and this is the following.

Eq. (2.4), (2.5) and "the converse of (2.5)" (that is $"\!\!b\lor c\ true\!\!" \implies "\!\!b\ true\!\!"\ or \ "\!\!c \ true\!\!"$) together would mean that the lattice "$(\mathscr L,\lor,\land)$ is isomorphic to the lattice $(\mathscr L',or, and)$ where $\mathscr L'=\{"\!\!x\ true\!\!":x\in\mathscr L\}$, so, since $(\mathscr L',or, and)$ is distributive, $(\mathscr L,\lor,\land)$ is also distributive.