Suppose $F_{net}$ on a body is 0 (still it has torque). i.e. it is performing pure rotational motion.
Now I want to consider torque about any point that is not center of mass. Should I include acceleration due to angular acceleration and apply a pseudo torque at center.
I have searched everywhere about pseudo torque and everywhere it is applied only when the axis is linearly accelerating and not due to rotation. Why not tangential acceleration due to rotation is considered?
If the net force is zero, then torque as summed about any arbitrary point is going to be invariant (the same all over). See the transformation of the summation point from the center of mass C to some arbitrary point A below:
$$ \require{cancel} \boldsymbol{\tau}_A = \boldsymbol{\tau}_C + \cancel{ \boldsymbol{r}_{A/C} \times \boldsymbol{F}} $$
But I think you are asking about the coupled terms when expressing the equations of motion not at the center of mass. In this case, yes there is a component of torque that relates to the translation of the center of mass.
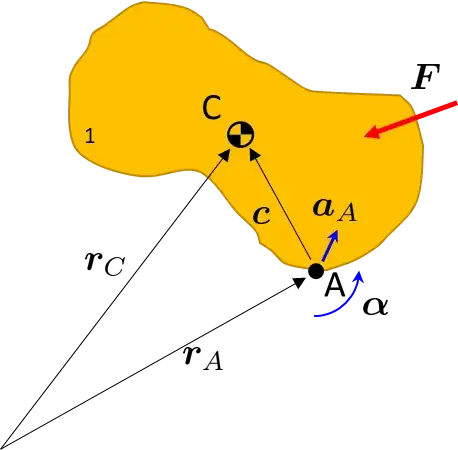
Take the equation of translation $\boldsymbol{F} = m \boldsymbol{a}_C$ and transform it to the arbitrary point. Consider the relative position vector of the center of mass $\boldsymbol{c} = \boldsymbol{r}_C - \boldsymbol{r}_A$ and form Newton's second law
$$ \boldsymbol{F} = m \left(\boldsymbol{a}_{A}-\boldsymbol{c}\times\boldsymbol{\alpha}+\boldsymbol{\omega}\times\left(\boldsymbol{\omega}\times\boldsymbol{c}\right) \right) \tag{1}$$
we will consider the special cases where forces are zero later. Now take the equation of rotation (Eule'r law) and consider the torque at A $\boldsymbol{\tau}_A = \boldsymbol{\tau}_C + \boldsymbol{c} \times \boldsymbol{F}$
$$ \boldsymbol{\tau}_A = {\bf I}_C \boldsymbol{\alpha} + \boldsymbol{\omega} \times {\bf I}_C \boldsymbol{\omega} + \boldsymbol{c} \times \boldsymbol{F} \tag{2}$$
So in general $\boldsymbol{\tau}_A$ has terms that depend on $\boldsymbol{a}_A$ when (1) is used in (2).
But if you know the net force $\boldsymbol{F}$ is zero, then the $\boldsymbol{c}\times \boldsymbol{F}$ term vanishes and you no longer have this cross dependency. This is in line with my first statement where $\boldsymbol{\tau}_A = \boldsymbol{\tau}_C$ with no net torque.
The reason we use the center of mass is exactly because it decouples the equations of motion
| Equations | At Center of Mass ($\boldsymbol{a}_C$, $\boldsymbol{\alpha}$, $\boldsymbol{F}$, $\boldsymbol{\tau}_C$) | At Arbitrary Point ($\boldsymbol{a}_A$, $\boldsymbol{\alpha}$, $\boldsymbol{F}$, $\boldsymbol{\tau}_A$) |
|---|---|---|
| Translation | $\boldsymbol{F} = m \boldsymbol{a}_C$ | $\boldsymbol{F} = m \left( \boldsymbol{a}_{A}-\boldsymbol{c}\times\boldsymbol{\alpha}+\boldsymbol{\omega}\times\left(\boldsymbol{\omega}\times\boldsymbol{c}\right) \right) $ |
| Rotation | $\boldsymbol{\tau}_C = {\bf I}_C \boldsymbol{\alpha} + \boldsymbol{\omega} \times {\bf I}_C \boldsymbol{\omega}$ | $\boldsymbol{\tau}_A = {\bf I}_C \boldsymbol{\alpha} + \boldsymbol{\omega} \times {\bf I}_C \boldsymbol{\omega} + \boldsymbol{c} \times \boldsymbol{F} $ |
The above is often expressed with linear algebra, using large 6×1 vectors that combine translational and rotational components into one. This is enabled by using the matrix form of the cross product
For example $ \boldsymbol{c} \times \boldsymbol{F} $ can be expressed as a matrix product as
$$ [\boldsymbol{c} \times] \boldsymbol{F} = \begin{bmatrix} 0 & -c_z & c_y \\ c_z & 0 & - c_x \\ -c_y & c_x & 0 \end{bmatrix} \begin{pmatrix} F_x \\ F_y \\ F_z \end{pmatrix}$$
where $[\boldsymbol{c} \times]$ is defined as the 3×3 skew-symmetric matrix derived from $\boldsymbol{c}$.
The above equations in matrix form and some re-arranging are
$$ \small \begin{Bmatrix}\boldsymbol{F}\\ \boldsymbol{\tau}_{A} \end{Bmatrix}=\begin{bmatrix}m[1] & -m[\boldsymbol{c}\times]\\ m[\boldsymbol{c}\times] & {\bf I}_{C}-m[\boldsymbol{c}\times][\boldsymbol{c}\times] \end{bmatrix}\begin{Bmatrix}\boldsymbol{a}_{A}\\ \boldsymbol{\alpha} \end{Bmatrix}+\begin{bmatrix}[1] & [0]\\{} [\boldsymbol{c}\times] & [1] \end{bmatrix}\begin{Bmatrix}\boldsymbol{\omega}\times m\left(\boldsymbol{\omega}\times\boldsymbol{c}\right)\\ \boldsymbol{\omega}\times{\bf I}_{C}\boldsymbol{\omega} \end{Bmatrix} \tag{3} $$
where $[0]$ is the zero 3×3 matrix, $[1]$ the identity matrix, and $[\boldsymbol{c}\times]$ as shown above. Also note that ${\bf I}_{A} = {\bf I}_{C}-m[\boldsymbol{c}\times][\boldsymbol{c}\times]$ is the parallel axis theorem in 3D vector form.
You might be interested in the inverse of the above, where you know the forces/torques and want to find out the motion of the arbitrary point
$$ \small \begin{Bmatrix}\boldsymbol{a}_{A}\\ \boldsymbol{\alpha} \end{Bmatrix}=\begin{bmatrix}\tfrac{1}{m}-[\boldsymbol{c}\times]{\bf I}_{C}^{-1}[\boldsymbol{c}\times] & [\boldsymbol{c}\times]{\bf I}_{C}^{-1}\\ -{\bf I}_{C}^{-1}[\boldsymbol{c}\times] & {\bf I}_{C}^{-1} \end{bmatrix}\left(\begin{Bmatrix}\boldsymbol{F}\\ \boldsymbol{\tau}_{A} \end{Bmatrix}-\begin{bmatrix}[1] & [0]\\{} [\boldsymbol{c}\times] & [1] \end{bmatrix}\begin{Bmatrix}\boldsymbol{\omega}\times m\left(\boldsymbol{\omega}\times\boldsymbol{c}\right)\\ \boldsymbol{\omega}\times{\bf I}_{C}\boldsymbol{\omega} \end{Bmatrix}\right) \tag{4} $$
From the above you can see that $[\boldsymbol{c}\times]{\bf I}_{C}^{-1}$ is the term relating torque at A $\boldsymbol{\tau}_A$ to acceleration at A $\boldsymbol{a}_A$.
There seems to be much confusion in answers provided on this exchange related to numerous questions about torques from fictitious forces in non-inertial frames.
Some answers claim that in the non-inertial frame the fictitious torques can be considered to always act at the center of mass; this is not true. Consider a rod on a fixed pivot on its center of mass (CM) with a force F applied at one end. With respect to the CM, in the inertial frame the force provides a torque hence a change in angular momentum of the rod. Viewed from a non-inertial frame where the rod is at rest, the angular momentum with respect to the CM is zero hence the total torque is zero meaning that a fictitious force creates a torque to counterbalance the torque from the applied force F. That fictitious torque cannot be assumed to act the CM.
See my answer at Where does pseudo force act at? where I attempt to provide a comprehensive answer.
Pseudo forces and pseudo torques are imaginary forces ( torques ) that appear in accelerated frames, and are used to compensate for the fact that $\vec F \neq m\vec a$ and $\vec \tau \neq \dot{\vec L}$ in non-inertial frames .
Simply choosing another inertial reference origin does not require pseudo torque because $\vec F = m\vec a$ and $\vec \tau = \dot{\vec L}$ from any chosen inertial origin.
If $\vec F = 0$ and $\vec \tau \neq 0$ then there at least two forces acting on the body. $$\vec \tau =\dot{ \vec L}= \sum \vec r_i \times \vec F_i$$ from any/all chosen inertial origins. The $\vec r_i$ change, but the forces stay the same. $\vec P$ And $\vec L$ are conserved.
